题目内容
【题目】直线l：ax+
y﹣1=0与x，y轴的交点分别为A，B，直线l与圆O：x2+y2=1的交点为C，D，给出下面三个结论：①a≥1，S△AOB=
；②a≥1，|AB|＜|CD|；③a≥1，S△COD＜.其中，所有正确结论的序号是（ ）
A.①②B.②③C.①③D.①②③
【答案】C
【解析】
①当a≥1时，分别可得直线的截距，由三角形的面积公式易得结论①正确；②当a≥1时，反证法可得结论②错误；③由三角形的面积公式可得S△COD
sin∠AOC
，可得结论③正确．
解：①当a≥1时，把x＝0代入直线方程可得y＝a，把y＝0代入直线方程可得x
，
∴S△AOB
a
，故结论①正确；
②当a≥1时，|AB|
，故|AB|2＝a2
，
直线l可化为a2x+y﹣a＝0，圆心O到l的距离d
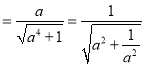，故|CD|2＝4（1﹣d2）＝4（1
），
假设|AB|＜|CD|，则|AB|2＜|CD|2，即a2
4（1），
整理可得（a2）2﹣4（a2）+4＜0，即（a2
2）2＜0，
显然矛盾，故结论②错误；
S△COD|OA||OC|sin∠AOCsin∠AOC，
故a≥1，使得S△COD
，结论③正确．
故选：C．
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
【题目】某市《城市总体规划（
年）》提出到
年实现“
分钟社区生活圈”全覆盖的目标，从教育与文化、医疗与养老、交通与购物、休闲与健身
个方面构建“分钟社区生活圈”指标体系，并依据“分钟社区生活圈”指数高低将小区划分为：优质小区（指数为
）、良好小区（指数为
）、中等小区（指数为
）以及待改进小区（指数为
）个等级.下面是三个小区个方面指标的调查数据：
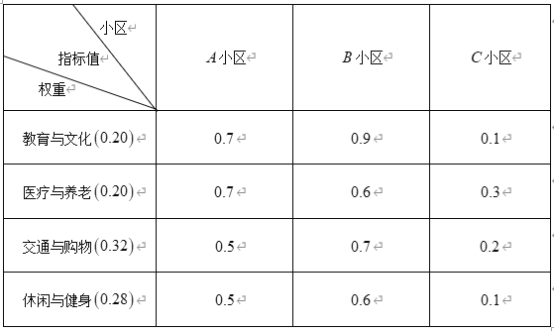
注：每个小区“分钟社区生活圈”指数
，其中
、
、
、
为该小区四个方面的权重，
、
、
、
为该小区四个方面的指标值（小区每一个方面的指标值为
之间的一个数值）.
现有
个小区的“分钟社区生活圈”指数数据，整理得到如下频数分布表：
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
（Ⅰ）分别判断
、
、
三个小区是否是优质小区，并说明理由；
（Ⅱ）对这个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样，抽取
个小区进行调查，若在抽取的个小区中再随机地选取
个小区做深入调查，记这个小区中为优质小区的个数
，求的分布列及数学期望.
