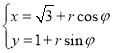题目内容
【题目】已知命题P：函数
且|f（a）|＜2，命题Q：集合A={x|x2+（a+2）x+1=0，x∈R}，B={x|x＞0}且A∩B=，
（1）分别求命题P、Q为真命题时的实数a的取值范围；
（2）当实数a取何范围时，命题P、Q中有且仅有一个为真命题；
（3）设P、Q皆为真时a的取值范围为集合S，
，若RTS，求m的取值范围.
【答案】（1）a∈（﹣4，+∞）；（2）a∈（﹣5，﹣4]∪[7，+∞）；（3）m∈（0，4]
【解析】
（1）由题意可得，由|f（a）|＝|
|＜2解不等式可得P：a∈（﹣5，7）；由A∩B＝，可得A有两种情况①若A＝，则△＝（a+2）（a+2）﹣4＜0，②若A≠φ，则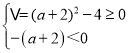
，解可得Q；
（2）当P为真，则
；当Q为真，则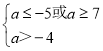
可求
（3）当P，Q都为真时，
可求S＝（﹣4，7），利用基本不等式可求T，进而可求RT，然后根据RTS，可求
解：（1）由题意可得，由|f（a）|＝||＜2可得﹣6＜a﹣1＜6
解可得，﹣5＜a＜7
∴P：a∈（﹣5，7）
∵集合A＝{x|x2+（a+2）x+1＝0，x∈R}，B＝{x|x＞0}且A∩B＝，
①若A＝，则△＝（a+2）（a+2）﹣4＜0，即﹣4＜a＜0
②若A≠φ，则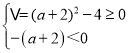，解可得，a≥0
综上可得，a＞﹣4
∴Q：a∈（﹣4，+∞）
（2）当P为真，则，a∈（﹣5，﹣4]；
当Q为真，则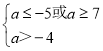，a∈[7，+∞）
所以a∈（﹣5，﹣4]∪[7，+∞）
（3）当P，Q都为真时，即S＝（﹣4，7）
∵
∴
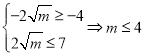
综上m∈（0，4]
练习册系列答案
相关题目
