题目内容
【题目】已知函数![]() .
.
(1)求![]() 的单调区间与极值;
的单调区间与极值;
(2)当函数![]() 有两个极值点时,求实数a的取值范围.
有两个极值点时,求实数a的取值范围.
【答案】(1)减区间![]() ,增区间
,增区间 ![]() ,极小值为
,极小值为![]() ,无极大值;(2)
,无极大值;(2)![]() .
.
【解析】
(1)求出函数![]() 的导函数,根据导函数即可求出单调区间以及极值;
的导函数,根据导函数即可求出单调区间以及极值;
(2)求出![]() 的导函数,使导函数有两个根,采用分离参数法,结合(1)中的值域即可求出参数的取值范围.
的导函数,使导函数有两个根,采用分离参数法,结合(1)中的值域即可求出参数的取值范围.
解:(1)由![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
因为函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以函数在![]() 处取得极小值,
处取得极小值,![]() 极小值
极小值![]() ,无极大值.
,无极大值.
综上所述,单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;![]() 极小值为2,无极大值;
极小值为2,无极大值;
(2)由![]() ,
,
则![]() ,
,
若![]() 有两个极值点,则
有两个极值点,则![]() 有两个根
有两个根
即![]() 有两解,即
有两解,即![]() ,
,
即![]() 与
与![]() 有两个交点,
有两个交点,
由(1)可知![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增,
上单调递增,
![]() ,所以
,所以![]() ;
;
考虑函数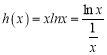 ,
,![]() ,
,
由洛必达法则: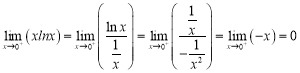 ,
,
![]() ,
,![]() ,
,
![]()
所以若![]() 与
与![]() 有两个交点,则
有两个交点,则![]() .
.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】随着小汽车的普及,“驾驶证”已经成为现代人“必考”的证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,他需要通过四个科目的考试,其中科目二为场地考试.在一次报名中,每个学员有5次参加科目二考试的机会(这5次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试;若5次都没有通过,则需重新报名),其中前2次参加科目二考试免费,若前2次都没有通过,则以后每次参加科目二考试都需要交200元的补考费.某驾校对以往2000个学员第1次参加科目二考试进行了统计,得到下表:
考试情况 | 男学员 | 女学员 |
第1次考科目二人数 | 1200 | 800 |
第1次通过科目二人数 | 960 | 600 |
第1次未通过科目二人数 | 240 | 200 |
若以上表得到的男、女学员第1次通过科目二考试的频率分别作为此驾校男、女学员每次通过科目二考试的概率,且每人每次是否通过科目二考试相互独立.现有一对夫妻同时在此驾校报名参加了驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)若这对夫妻前2次参加科目二考试均没有通过,记这对夫妻在本次报名中参加科目二考试产生的补考费用之和为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() ,
,![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在![]() ,
,![]() 试验地随机抽选各
试验地随机抽选各![]() 株,对每株进行综合评分(评分的高低反映花苗品质的高低),将每株所得的综合评分制成如图所示的频率分布直方图:
株,对每株进行综合评分(评分的高低反映花苗品质的高低),将每株所得的综合评分制成如图所示的频率分布直方图:
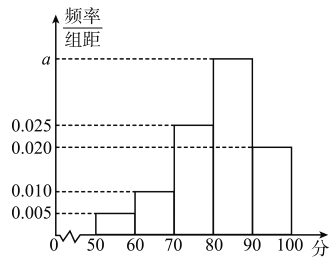
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)记综合评分为![]() 及以上的花苗为优质花苗.填写下面的列联表,并判断是否有
及以上的花苗为优质花苗.填写下面的列联表,并判断是否有![]() 的把握认为优质花苗与培育方法有关.
的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 |
| ||
乙培育法 |
| ||
合计 |
附:下面的临界值表仅供参考.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式: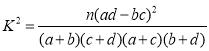 ,其中
,其中![]() .)
.)
【题目】环保部门要对所有的新车模型进行广泛测试,以确定它的行车里程的等级,下表是对100辆新车模型在一个耗油单位内行车里程(单位:公里)的测试结果.
分组 | 频数 |
| 6 |
| 10 |
| 20 |
| 30 |
| 18 |
| 12 |
| 4 |
(1)做出上述测试结果的频率分布直方图,并指出其中位数落在哪一组;
(2)用分层抽样的方法从行车里程在区间![]() 与
与![]() 的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在
的新车模型中任取5辆,并从这5辆中随机抽取2辆,求其中恰有一个新车模型行车里程在![]() 内的概率.
内的概率.