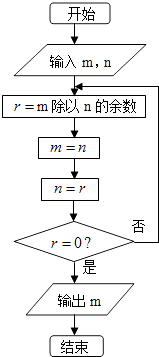
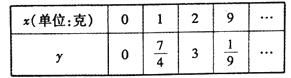
题目内容
【题目】一条光线从点![]() 射出,经
射出,经![]() 轴反射后与圆
轴反射后与圆![]() 相交于点
相交于点![]() ,且
,且![]() ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.
【答案】![]() 和
和![]() .
.
【解析】试题分析:当反射光线的斜率不存在时,反射光线所在的直线方程为![]() ;当反射光线的斜率存在时,设反射光线直线方程
;当反射光线的斜率存在时,设反射光线直线方程![]() ,利用点到直线的距离公式,求解
,利用点到直线的距离公式,求解![]() 的值,即可得到直线的方程.
的值,即可得到直线的方程.
试题解析:
点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,
,
(![]() )当反射光线的斜率不存在时,反射光线所在的直线方程为:
)当反射光线的斜率不存在时,反射光线所在的直线方程为: ![]() ,
,
此时,圆心![]() 到反射光线的距离为
到反射光线的距离为![]() ,且圆的半径为
,且圆的半径为![]() ,
,
所以反射光线被圆所截得的弦长![]() ,符合题意.
,符合题意.
(![]() )当反射光线的斜率存在时,设反射光线的斜率为
)当反射光线的斜率存在时,设反射光线的斜率为![]() ,则反射光线所在的直线方程为
,则反射光线所在的直线方程为![]() 即
即![]() .
.
因为反射光线被圆所截得的弦长![]() ,且圆的半径为
,且圆的半径为![]() ,
,
所以圆心到反射光线的距离为 .
.
而圆心![]() 到反射光线的距离
到反射光线的距离![]() ,
,
即![]() ,解得
,解得![]() .
.
所以反射光线所在的直线方程为![]() 即
即![]() .
.
综上,反射光线所在的直线方程为![]() 和
和![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目