Question

【题目】如图所示，已知抛物线C：y2＝4x的焦点为F，直线l经过点F且与抛物线C相交于A、B两点．

(1)若线段AB的中点在直线y＝2上，求直线l的方程；

(2)若线段|AB|＝20，求直线l的方程．

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）设直线l的斜率为k，A(x1，y1)，B(x2，y2)，AB的中点M(x0，y0)，由点差法，可得2y0k＝4，又，所以。（2）设直线l的方程为x＝my＋1，与抛物线联立组方程组，由弦长公式与志达定理，可求得参数m的值.

试题解析：(1)由已知得抛物线的焦点为F(1,0)．因为线段AB的中点在直线y＝2上，所以直线l的斜率存在，设直线l的斜率为k，A(x1，y1)，B(x2，y2)，AB的中点M(x0，y0)，

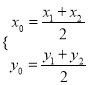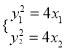则由得

(y1＋y2)(y1－y2)＝4(x1－x2)，所以2y0k＝4.

又y0＝2，所以k＝1，故直线l的方程是y＝x－1.

(2)设直线l的方程为x＝my＋1，与抛物线方程联立得消元得y2－4my－4＝0，所以y1＋y2＝4m，y1y2＝－4，Δ＝16(m2＋1)>0.

|AB|＝|y1－y2|＝·

＝·＝4(m2＋1)．

所以4(m2＋1)＝20，解得m＝±2，

所以直线l的方程是x＝±2y＋1，

即x±2y－1＝0.