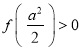题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆E的长轴和短轴为对角线的四边形的面积为
,以椭圆E的长轴和短轴为对角线的四边形的面积为![]() .
.
(1)求椭圆E的方程;
(2)若直线![]() 与椭圆E相交于A,B两点,设P为椭圆E上一动点,且满足
与椭圆E相交于A,B两点,设P为椭圆E上一动点,且满足![]() (O为坐标原点).当
(O为坐标原点).当![]() 时,求
时,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由离心率及四边形的面积和a,b,c之间的关系求出椭圆的方程;
(2)将直线与椭圆联立求出两根之和及两根之积,![]() ,可得
,可得![]() .进而写出P的坐标,P在椭圆上求出m的范围,进而求出
.进而写出P的坐标,P在椭圆上求出m的范围,进而求出![]() 的表达式,由反比例函数的单调性求出它的最小值.
的表达式,由反比例函数的单调性求出它的最小值.
解:(1)依题意得,![]() .以椭圆E的长轴和短轴为对角线的四边形的面积为
.以椭圆E的长轴和短轴为对角线的四边形的面积为![]() ,则
,则![]() ,解得
,解得![]() ,
,![]() .
.
所以椭圆E的方程为![]() .
.
(2)设A,B两点的坐标分别为![]() ,
,
联立方程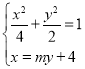 得
得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
因为![]() ,即
,即![]() ,所以
,所以![]() .
.
所以点![]() ,又点P在椭圆C上,所以有
,又点P在椭圆C上,所以有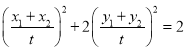 ,
,
化简得![]() ,
,
所以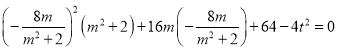 ,化简
,化简![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 取得最小值,最小值为
取得最小值,最小值为![]() .
.

【题目】某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.

组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) |
| 0.9 |
第3组 | [35,45) | 27 |
|
第4组 | [45,55) |
| 0.36 |
第5组 | [55,65) | 3 |
|
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
【题目】我国在2018年社保又出新的好消息,之前流动就业人员跨地区就业后,社保转移接续的手续往往比较繁琐,费时费力.社保改革后将简化手续,深得流动就业人员的赞誉.某市社保局从2018年办理社保的人员中抽取300人,得到其办理手续所需时间(天)与人数的频数分布表:
时间 |
|
|
|
|
|
|
人数 | 15 | 60 | 90 | 75 | 45 | 15 |
(1)若300名办理社保的人员中流动人员210人,非流动人员90人,若办理时间超过4天的人员里非流动人员有60人,请完成办理社保手续所需时间与是否流动人员的列联表,并判断是否有95%的把握认为“办理社保手续所需时间与是否流动人员”有关.
列联表如下
流动人员 | 非流动人员 | 总计 | |
办理社保手续所需 时间不超过4天 | |||
办理社保手续所需 时间超过4天 | 60 | ||
总计 | 210 | 90 | 300 |
(2)为了改进工作作风,提高效率,从抽取的300人中办理时间为![]() 流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为
流动人员中利用分层抽样,抽取12名流动人员召开座谈会,其中3人要求交书面材料,3人中办理的时间为![]() 的人数为
的人数为![]() ,求出
,求出![]() 分布列及期望值.
分布列及期望值.
附: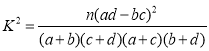
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |