题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)据题意,得 ,求解方程组确定a,b的值即可求得椭圆方程;
,求解方程组确定a,b的值即可求得椭圆方程;
(2)据题设知点![]() ,当直线
,当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .与椭圆方程联立,结合韦达定理有
.与椭圆方程联立,结合韦达定理有![]() . 假设存在点M满足题意,则
. 假设存在点M满足题意,则![]() ,结合韦达定理求解实数m的值即可;然后讨论斜率不存在的情况即可确定定点M存在.
,结合韦达定理求解实数m的值即可;然后讨论斜率不存在的情况即可确定定点M存在.
(1)据题意,得
解得![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)据题设知点![]() ,当直线
,当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由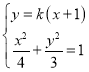 ,得
,得![]() .
.
设![]() ,则
,则![]() .
.
设![]() ,则直线
,则直线![]() 的斜率分别满足
的斜率分别满足![]() .
.
又因为直线![]() 的斜率互为相反数,
的斜率互为相反数,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以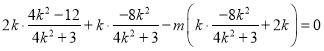 ,所以
,所以![]() .
.
若![]() 对任意
对任意![]() 恒成立,则
恒成立,则![]() ,
,
当直线![]() 的斜率
的斜率![]() 不存在时,若
不存在时,若![]() ,则点
,则点![]() 满足直线
满足直线![]() 的斜率互为相反数.
的斜率互为相反数.
综上,在![]() 轴上存在一个定点
轴上存在一个定点![]() ,使得直线
,使得直线![]() 的斜率互为相反数.
的斜率互为相反数.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
【题目】为了解高一年级学生的智力水平,某校按1:10的比例对700名高一学生按性别分别进行“智力评分”抽样调查,测得“智力评分”的频数分布表如表1、表2所示.
表1:男生“智力评分”频数分布表
智力评分/分 |
|
|
|
|
|
|
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生“智力评分”频数分布表
智力评分/分 |
|
|
|
|
|
|
频数 | 1 | 7 | 12 | 6 | 3 | 1 |

(1)求高一年级的男生人数,并完成下面男生“智力评分”的频率分布直方图;
(2)估计该校高一年级学生“智力评分”在![]() 内的人数.
内的人数.

