题目内容
【题目】已知函数![]()
![]() 的最大值是0,函数
的最大值是0,函数![]()
![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)求出函数的导函数,根据函数的单调性求出f(x)的最大值,得到关于m的方程,进而求出m的值;
(Ⅱ)构造函数F(x)=f(x)-g(x),求出函数的导函数![]() ,进而求出
,进而求出![]() 的导函数
的导函数![]() ,利用导数与函数单调性的关系,通过讨论a的范围,得到函数的单调区间,结合函数恒成立问题,进而求出a的取值范围.
,利用导数与函数单调性的关系,通过讨论a的范围,得到函数的单调区间,结合函数恒成立问题,进而求出a的取值范围.
(Ⅰ)函数![]() 的定义域为
的定义域为![]()
![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
令![]() ,得
,得![]()
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减;
单调递减;
所以,当![]() 时,
时,![]() =
=![]()
于是,![]() ,得
,得![]() ,
,
易知,函数![]() 在
在![]() 处有唯一零点,所以
处有唯一零点,所以![]() ,
,![]() .
.
(Ⅱ)令![]() ,
,![]()
则![]() ,
,
设![]()
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
则![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
故当![]() 时,
时,![]() ,与已知矛盾.
,与已知矛盾.
②当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
则![]() 时,
时,![]()
故![]() 在
在![]() 上单调递减,
上单调递减,
则当![]() 时,
时,![]() ,与已知矛盾.
,与已知矛盾.
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
则![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增,故当
上单调递增,故当![]() 时,
时,![]() 恒成立.
恒成立.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
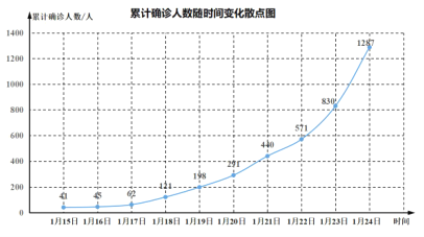
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为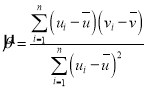 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
【题目】某研究公司为了调查公众对某事件的关注程度,在某年的连续6个月内,月份![]() 和关注人数
和关注人数![]() (单位:百)(
(单位:百)(![]() )数据做了初步处理,得到下面的散点图及一些统计量的值.
)数据做了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
17.5 | 35 | 36.5 |
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明,并建立y关于x的回归方程;
(2)经统计,调查材料费用v(单位:百元)与调查人数满足函数关系![]() ,求材料费用的最小值,并预测此时的调查人数;
,求材料费用的最小值,并预测此时的调查人数;
(3)现从这6个月中,随机抽取3个月份,求关注人数不低于1600人的月份个数![]() 分布列与数学期望.
分布列与数学期望.
参考公式:相关系数 ,若
,若![]() ,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为 ,
,![]() .
.