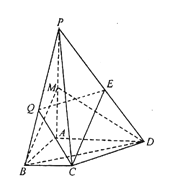
题目内容
【题目】一个正方形被剖分为4个正方形，剖分图的边数为12.若一个正方形被剖分为2005个凸多边形，试求剖分图中边数的最大值.
【答案】正方形剖分为2005个凸多边形时，边的最大值为6016.
【解析】
由欧拉定理可知，简单多面体的顶点数
、面数
、棱数
有如下关系：
.
由欧拉定理容易看出，若一个凸多边形被剖分为
个凸多边形，则剖分图中的顶点数、多边形数、边数满足
. ①
下面在一般的情况下，即正方形被剖分为个凸多边形时，求剖分图中边数的最大值.设剖分图中的顶点数为、多边形数为、边数为.
（1）先求边数的上界.
设原正方形的4个顶点是
、
、
、
.若凸多边形的顶点
，则易知
（这里用
表示过顶点
的边数）.
故
.
注意到这样的顶点有
个，于是，有个上面的不等式.将它们相加求和，并注意到除去正方形四边的每条边恰是两个凸多边形的边，有
.
即
.
因为
，
，
，
.
则
. ②
由式①有
.
将式②代入式③，并整理得
，即
.
（2）构造例子，使边数
.
如图，过正方形的一边相继作
条邻边的平行线，正方形被剖分为个矩形，易知，边数
.
综上所述，剖分图中边数的最大值为
.
所以，正方形剖分为2005个凸多边形时，边的最大值为6016.
【题目】某工厂共有男女员工500人，现从中抽取100位员工对他们每月完成合格产品的件数统计如下：
每月完成合格产品的件数（单位：百件） |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
（1）其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面
列联表，并判断是否有95%的把握认为“生产能手”与性别有关？
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
span>女员工 | |||
合计 |
（2）为提高员工劳动的积极性，工厂实行累进计件工资制：规定每月完成合格产品的件数在定额2600件以内的，计件单价为1元；超出
件的部分，累进计件单价为1.2元；超出
件的部分，累进计件单价为1.3元；超出400件以上的部分，累进计件单价为1.4元.将这4段中各段的频率视为相应的概率，在该厂男员工中选取1人，女员工中随机选取2人进行工资调查，设实得计件工资（实得计件工资=定额计件工资+超定额计件工资）不少于3100元的人数为，求的分布列和数学期望.
附：
，
.
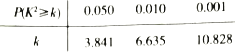【题目】《中华人民共和国民法总则》（以下简称《民法总则》）自2017年10月1日起施行.作为民法典的开篇之作，《民法总则》与每个人的一生息息相关.某地区为了调研本地区人们对该法律的了解情况，随机抽取50人，他们的年龄都在区间
上，年龄的频率分布及了解《民法总则》的入数如下表：
年龄 |
|
|
|
|
|
|
频数 | 5 | 5 | 10 | 15 | 5 | 10 |
了解《民法总则》 | 1 | 2 | 8 | 12 | 4 | 5 |
（1）填写下面
列联表，并判断是否有
的把握认为以45岁为分界点对了解《民法总则》政策有差异；
年龄低于45岁的人数 | 年龄不低于45岁的人数 | 合计 | |
了解 |
|
| |
不了解 |
|
| |
合计 |
（2）若对年龄在
，
的被调研人中各随机选取2人进行深入调研，记选中的4人中不了解《民法总则》的人数为
，求随机变量的分布列和数学期望.
参考公式和数据：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
