题目内容
【题目】将边长为正整数m、n的矩形划分成若干边长均为正整数的正方形,每个正方形的边均平行于矩形的相应边,试求这些正方形边长之和的最小值.

【答案】![]()
【解析】
记所求最小值为![]() ,可以证明
,可以证明![]() .(*)
.(*)
事实上,不妨设![]() .
.
(1)对m归纳,可证明存在一种合乎题意的分法,使所得正方形边长之和恰为![]() .
.
当m=1,时,命题显然成立.
假设当![]() 时,结论成立
时,结论成立![]() .当
.当![]() 时,若
时,若![]() ,则命题显然成立,若
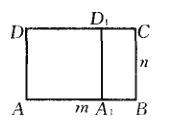
,则命题显然成立,若![]() ,从矩形ABCD中切去正方形
,从矩形ABCD中切去正方形![]() (如图).由归纳假设,矩形
(如图).由归纳假设,矩形![]() 有一种分法使得所得正方形边长之和恰为
有一种分法使得所得正方形边长之和恰为![]() .
.
于是,原矩形ABCD有一种分法使得所得正方形边长之和为![]() .
.
(2)对m归纳可以证明(*)成立.
当m=1时,由于n=1,显然![]() .
.
假设当![]() 时,对任意
时,对任意![]() ,有
,有![]() .
.
若![]() ,当
,当![]() 时,显然
时,显然![]()
当![]() 时,设矩形ABCD按要求分成了p个正方形,其边长分别为
时,设矩形ABCD按要求分成了p个正方形,其边长分别为![]() .不妨设
.不妨设![]() .
.
显然,![]() 或
或![]() .
.
若![]() ,则在AD与BC之间的与AD平行的任一直线至少穿过二个分成的正方形(或其边界),于是
,则在AD与BC之间的与AD平行的任一直线至少穿过二个分成的正方形(或其边界),于是![]() 不少于AB与CD之和.
不少于AB与CD之和.
故![]() .
.
若![]() ,则一个边长分别为m-n和n的矩形可按题目要求分成边长分别为
,则一个边长分别为m-n和n的矩形可按题目要求分成边长分别为![]() 的正方形,由归纳假设
的正方形,由归纳假设![]() .
.
从而,![]()
于是,当m=k+1时,![]()
再由(1)可知,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
