题目内容
1．不等式$\frac{{{x^2}+2x-3}}{x+1}$≤0的解集为（ ）| A． | {x|x≥3或-1≤x≤1} | B． | {x|x≥3或-1＜x≤1} | C． | {x|x≤-3或-1≤x≤1} | D． | {x|x≤-3或-1＜x≤1} |
分析 不等式即 $\frac{（x+3）（x-1）}{x+1}$≤0，再用穿根法求得它的解集．
解答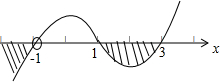 
解：不等式$\frac{{{x^2}+2x-3}}{x+1}$≤0，即 $\frac{（x+3）（x-1）}{x+1}$≤0，
用穿根法求得它的解集为{x|x≤-3或-1＜x≤1}，
故选：D．
点评 本题主要考查用穿根法求分式不等式的解集，体现了转化、数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
12．设x为实数，命题p：?x∈R，x2+x+1≥0的否定是（ ）
| A． | ￢p：?x0∈R，x02+x0+1＜0 | B． | ￢p：?x0∈R，x02+x0+1≤0 | ||
| C． | ￢p：?x0∈R，x02+x0+1＜0 | D． | ￢p：?x0∈R，x02+x0+1≤0 |
9．不等式$\frac{{-{x^2}-2x+3}}{x+1}$≥0的解集为（ ）
| A． | {x|x≥3或-1≤x≤1} | B． | {x|x≥3或-1＜x≤1} | C． | {x|x≤-3或-1≤x≤1} | D． | {x|x≤-3或-1＜x≤1} |
16．已知不等式$\frac{x-3}{ax+b}$＞0的解集为（-1，3），那么$\frac{{{a^3}-2{b^3}}}{{3{b^2}a}}$=（ ）
| A． | 3 | B． | -$\frac{1}{3}$ | C． | -1 | D． | 1 |
6．函数f（x）=-x3+ax在[0，+∞）上是减函数，则a的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，0] | C． | （0，+∞） | D． | [0，+∞） |
10．如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（ ）
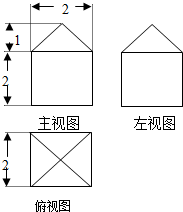
| A． | $（20+4\sqrt{3}）c{m^2}$ | B． | $（20+4\sqrt{2}）c{m^2}$ | C． | $（20+\sqrt{2}）c{m^2}$ | D． | $（10+4\sqrt{2}）c{m^2}$ |