题目内容
(本题12分)一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇).
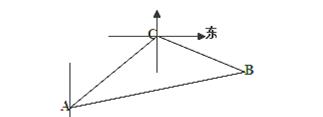

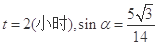 .
. 本题考查正余弦定理在实际问题中的运用,关键是构建三角形,寻找边角关系,属于基础题.
(1)设缉私艇追上走私船所需的时间为t小时,在△ABC中利用正弦定理可求;
(2)在△ABC中利用余弦定理可求追击所需的时间,解方程24t2-15t-9=0可得.
解:设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇,由条件知∠ABC=120°,AB=12(海里),设t小时后追及,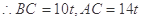 ,
,
由正弦定理得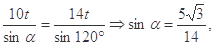 ;
;
再由余弦定理得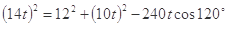
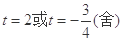 ,
,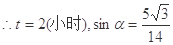 .
.
(1)设缉私艇追上走私船所需的时间为t小时,在△ABC中利用正弦定理可求;
(2)在△ABC中利用余弦定理可求追击所需的时间,解方程24t2-15t-9=0可得.
解:设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇,由条件知∠ABC=120°,AB=12(海里),设t小时后追及,
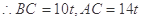 ,
,由正弦定理得
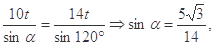 ;
;再由余弦定理得
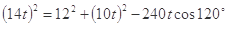
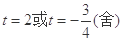 ,
,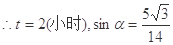 .
. 
练习册系列答案
相关题目
 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且
 =4,
=4, ,求
,求 的值.
的值.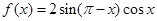 .
.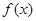 的最小正周期;
的最小正周期;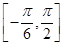 上的最大值和最小值.
上的最大值和最小值. 的三个内角
的三个内角 的对边分别为
的对边分别为 ,已知
,已知 成等比数列,且
成等比数列,且

 的大小;
的大小;  ,求函数
,求函数 的值域.
的值域.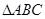 中,点
中,点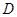 在
在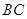 边上,
边上,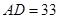 ,
,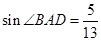 ,
,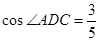 .
.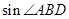 的值;
的值;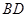 的长.
的长. 
 中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2
中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2 -1)=-
-1)=- cos2B.
cos2B. ,求
,求 的最大值.
的最大值. .
. ,求
,求 面积的最大值.
面积的最大值. 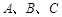 所对的边分别为
所对的边分别为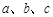 ,边a、b是方程x2-2
,边a、b是方程x2-2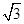 x +2=0的两根,角A、B满足关系2sin(A+B)-
x +2=0的两根,角A、B满足关系2sin(A+B)- 中,
中, 则
则 的值为( )
的值为( )


