题目内容
(本题满分14分 )在锐角 中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2
中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2 -1)=-
-1)=- cos2B.
cos2B.
(1)求B的大小;
(2)如果 ,求
,求 的面积
的面积 的最大值.
的最大值.
 中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2
中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2 -1)=-
-1)=- cos2B.
cos2B.(1)求B的大小;
(2)如果
 ,求
,求 的面积
的面积 的最大值.
的最大值.(1)B=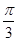 ;(2)△ABC的面积最大值为
;(2)△ABC的面积最大值为 。
。
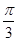 ;(2)△ABC的面积最大值为
;(2)△ABC的面积最大值为 。
。(1)由2sinB(2cos2 -1)=-
-1)=- cos2B可得2sinBcosB=-
cos2B可得2sinBcosB=- cos2B,从而得tan2B=-
cos2B,从而得tan2B=- ,得2B=
,得2B=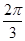 ,∴B=
,∴B=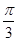 .
.
(2)由于B=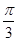 ,b=2,所以由余弦定理4=a2+c2-ac≥2ac-ac=ac,从而得出ac的最大值为4,故面积最大值确定.
,b=2,所以由余弦定理4=a2+c2-ac≥2ac-ac=ac,从而得出ac的最大值为4,故面积最大值确定.
解:(1)2sinB(2cos2 -1)=-
-1)=- cos2BÞ2sinBcosB=-
cos2BÞ2sinBcosB=- cos2B Þ tan2B=-
cos2B Þ tan2B=- ……4分
……4分
∵0<2B<π,∴2B=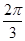 ,∴B=
,∴B=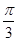 ……6分
……6分
(2)由tan2B=- Þ B=
Þ B=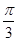
∵b=2,由余弦定理,得:4=a2+c2-ac≥2ac-ac=ac(当且仅当a=c=2时等号成立)……10
∵△ABC的面积S△ABC=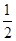 acsinB=
acsinB=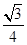 ac≤
ac≤
∴△ABC的面积最大值为 ……14
……14
 -1)=-
-1)=- cos2B可得2sinBcosB=-
cos2B可得2sinBcosB=- cos2B,从而得tan2B=-
cos2B,从而得tan2B=- ,得2B=
,得2B=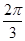 ,∴B=
,∴B=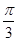 .
.(2)由于B=
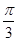 ,b=2,所以由余弦定理4=a2+c2-ac≥2ac-ac=ac,从而得出ac的最大值为4,故面积最大值确定.
,b=2,所以由余弦定理4=a2+c2-ac≥2ac-ac=ac,从而得出ac的最大值为4,故面积最大值确定.解:(1)2sinB(2cos2
 -1)=-
-1)=- cos2BÞ2sinBcosB=-
cos2BÞ2sinBcosB=- cos2B Þ tan2B=-
cos2B Þ tan2B=- ……4分
……4分 ∵0<2B<π,∴2B=
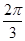 ,∴B=
,∴B=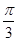 ……6分
……6分(2)由tan2B=-
 Þ B=
Þ B=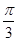
∵b=2,由余弦定理,得:4=a2+c2-ac≥2ac-ac=ac(当且仅当a=c=2时等号成立)……10
∵△ABC的面积S△ABC=
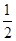 acsinB=
acsinB=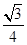 ac≤
ac≤
∴△ABC的面积最大值为
 ……14
……14
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
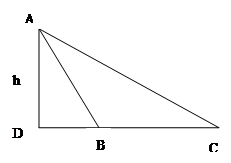
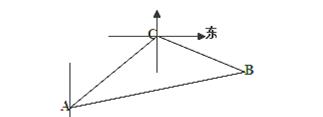
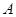 上测得正前方的河流的两岸
上测得正前方的河流的两岸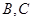 的俯角分别为
的俯角分别为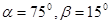 ,如果这时气球的高度
,如果这时气球的高度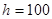 米,求河流的宽度
米,求河流的宽度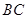 .
.
 -3
-3
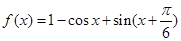 .
.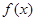 的最小正周期;
的最小正周期;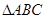 得内角
得内角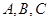 的对应边为
的对应边为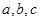 ,若
,若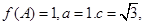 求
求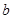 的值.
的值.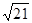 ,b=4,且BC边上的高h=
,b=4,且BC边上的高h=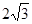 。
。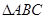 中,角A,B,C所对的边分别为a,b,c,已知
中,角A,B,C所对的边分别为a,b,c,已知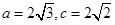 ,
,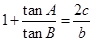 ,则
,则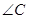 = _______
= _______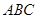 中,内角
中,内角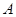 、
、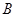 、
、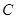 的对边分别为
的对边分别为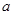 、
、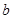 、
、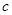 ,已知
,已知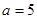 ,
,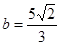 ,
,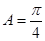 ,则
,则 。
。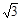 ,AB=2,则△ABC的面积为_________.
,AB=2,则△ABC的面积为_________.