题目内容
7.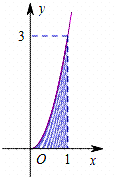 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )| A. | $\frac{99}{100}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
分析 利用阴影部分与矩形的面积比等于落入阴影部分的豆子数与所有豆子数的比,由此求出阴影部分的面积.
解答 解:由题意设阴影部分的面积为S,则$\frac{S}{3}=\frac{33}{100}$,所以S=$\frac{99}{100}$;
故选:A.
点评 本题考查了几何概型的应用;关键是明确落入阴影部分的豆子数与所有豆子的比等于阴影部分与矩形的面积比.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
18.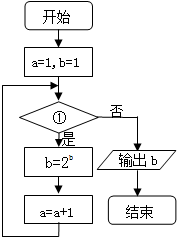 已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
 已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |
12.已知命题p:?x>0,x+$\frac{1}{x}$≥2,则¬p为( )
| A. | ?$x>0,\;\;x+\frac{1}{x}$<2 | B. | ?$x≤0,\;\;x+\frac{1}{x}$<2 | C. | ?$x≤0,\;\;x+\frac{1}{x}$<2 | D. | ?$x>0,\;\;x+\frac{1}{x}$<2 |
17.冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表所示.
根据以上数据,则( )
| 杂质高 | 杂质低 | |
| 旧设备 | 37 | 121 |
| 新设备 | 22 | 202 |
| A. | 含杂质的高低与设备改造有关 | B. | 含杂质的高低与设备改造无关 | ||
| C. | 设备是否改造决定含杂质的高低 | D. | 以上答案都不对 |
