题目内容
12.已知命题p:?x>0,x+$\frac{1}{x}$≥2,则¬p为( )| A. | ?$x>0,\;\;x+\frac{1}{x}$<2 | B. | ?$x≤0,\;\;x+\frac{1}{x}$<2 | C. | ?$x≤0,\;\;x+\frac{1}{x}$<2 | D. | ?$x>0,\;\;x+\frac{1}{x}$<2 |
分析 根据全称命题的否定是特称命题即可得到结论.
解答 解:命题p为全称命题,则命题的否定为:?$x>0,\;\;x+\frac{1}{x}$<2,
故选:D
点评 本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.设全集U=R,集合A={x|x-1>0},B={x|-x2+2x≤0},则A∩(CUB}=( )
| A. | {x|0<x≤1} | B. | {x|1≤x<1} | C. | {x|1<x<2} | D. | {x|1<x≤1} |
3.下列程序框表示一个算法输入和输出信息的是( )
| A. |  | B. |  | C. |  | D. |  |
7.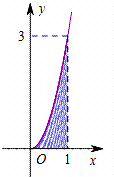 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )| A. | $\frac{99}{100}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
17.设a=0.23,b=log20.3,c=log0.32,则( )
| A. | b<a<c | B. | b<c<a | C. | c<b<a | D. | a<b<c |
4.在空间直角坐标系O-xyz,点P(1,2,3)关于xOy平面的对称点是( )
| A. | (-1,2,3) | B. | (-1,-2,3) | C. | (1,2,-3) | D. | (1,-2,-3) |
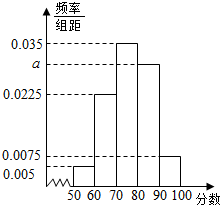 某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.
某班共有学生40人,将一次数学考试成绩(单位:分)绘制成频率分布直方图,如图所示.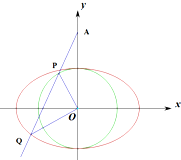 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,短轴端点在圆O:x2+y2=1上
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,短轴端点在圆O:x2+y2=1上