题目内容
2.给出下列四个结论:①存在实数$α∈(0,\frac{π}{2})$,使sinα+cosα=$\frac{1}{3}$
②函数y=1+sin2x是偶函数
③直线 x=$\frac{π}{8}$是函数$y=sin(2x+\frac{5}{4}π)$的一条对称轴方程
④若α、β都是第一象限的角,且α>β,则sinα>sinβ
其中正确结论的序号是②③.(写出所有正确结论的序号)
分析 根据三角函数的性质进行判断即可.
解答 解:①sinα+cosα=$\sqrt{2}$sin(α+$\frac{π}{4}$),α∈(0,$\frac{π}{4}$),
∴α=0或$\frac{π}{4}$时,取得最小值1,取不到$\frac{1}{3}$,故①错误;
②令x=-x,得y=1+sin2(-x)=1+sin2x,是偶函数,故②正确;
③当x=$\frac{π}{8}$时,函数y=sin($\frac{π}{4}$+$\frac{5}{4}$π)=sin$\frac{3π}{2}$=-1,故x=$\frac{π}{8}$是函数的一条对称轴,故③正确;
④若α=2π+$\frac{π}{4}$>β=$\frac{π}{3}$,但是sinα<sinβ,故④错误,
故答案为:②③.
点评 本题考查了三角函数的性质,是一道基础题.

练习册系列答案
相关题目
13.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x+y-1≤0}\\{x-y-1≤0}\\{x≥0}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
10.阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( )


| A. | 计算1+21+22+…+210的和 | B. | 计算1+21+22+…+29的和 | ||
| C. | 计算1+3+7+…+(29-1)的和 | D. | 计算1+3+7+…+(210-1)的和 |
17. 从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
(1)在答题卡上补全这些数据作出的频率分布直方图;
(2)估计这种产品质量指标值的平均值及方差(同一组中的数据用该组区间的中点值作代表);
(3)估计这种产品质量指标值的中位数.(精确到0.1)
 从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 28 | 34 | 24 | 8 |
(2)估计这种产品质量指标值的平均值及方差(同一组中的数据用该组区间的中点值作代表);
(3)估计这种产品质量指标值的中位数.(精确到0.1)
7.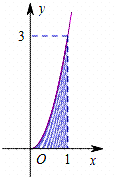 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
 已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )
已知函数f(x)的部分图象如图所示.向图中的矩形区域随机投出100粒豆子,记下落入阴影区域的豆子数.通过10次这样的试验,算得落入阴影区域的豆子的平均数约为33,由此可估计${∫}_{0}^{1}$f(x)dx的值约为( )| A. | $\frac{99}{100}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{10}{11}$ |
14.如图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.则①处可填写( )
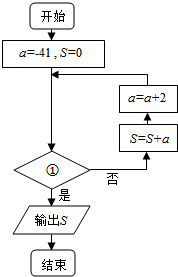

| A. | S>0 | B. | S<0 | C. | a>0 | D. | a=0 |