题目内容
(本小题满分12分)
在数列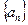 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈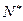 .
.
(1)设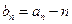 ,求数列
,求数列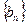 的通项公式;
的通项公式;
(2)设数列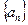 的前n项和为Sn,证明:对任意的n∈
的前n项和为Sn,证明:对任意的n∈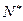 ,不等式Sn+1≤4Sn恒成立.
,不等式Sn+1≤4Sn恒成立.
在数列
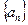 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈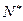 .
.(1)设
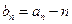 ,求数列
,求数列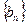 的通项公式;
的通项公式;(2)设数列
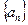 的前n项和为Sn,证明:对任意的n∈
的前n项和为Sn,证明:对任意的n∈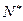 ,不等式Sn+1≤4Sn恒成立.
,不等式Sn+1≤4Sn恒成立.(Ⅰ)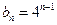 (Ⅱ) 见解析
(Ⅱ) 见解析
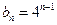 (Ⅱ) 见解析
(Ⅱ) 见解析(1)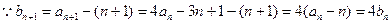

 ……3分
……3分
且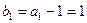 …………………………….…..……..4分
…………………………….…..……..4分
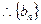 为以1为首项,以4为公比的等比数列
为以1为首项,以4为公比的等比数列
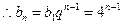 ……………………………………………………...5分
……………………………………………………...5分
(2) , ……………………………………6分
, ……………………………………6分
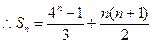 ………………………………………...8分
………………………………………...8分
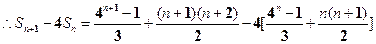
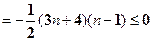 …………………………………11分
…………………………………11分
 …………………………12分
…………………………12分
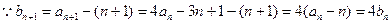

 ……3分
……3分且
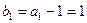 …………………………….…..……..4分
…………………………….…..……..4分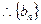 为以1为首项,以4为公比的等比数列
为以1为首项,以4为公比的等比数列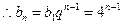 ……………………………………………………...5分
……………………………………………………...5分(2)
 , ……………………………………6分
, ……………………………………6分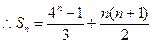 ………………………………………...8分
………………………………………...8分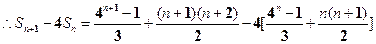
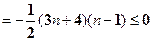 …………………………………11分
…………………………………11分 …………………………12分
…………………………12分
练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
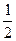 nan+an—c(c是常数,n∈N*),a2=6.
nan+an—c(c是常数,n∈N*),a2=6.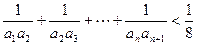
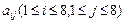 中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且
中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且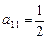 ,
,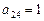 ,
,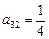 。
。 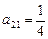 ,求
,求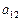 和
和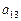 的值。
的值。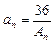 ,联
,联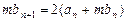 (m为非零常数),
(m为非零常数), ,且
,且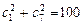 ,求
,求 的取值范围。
的取值范围。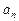 ,记
,记 ,设
,设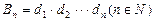 ,求数列
,求数列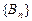 中最大项的项数。
中最大项的项数。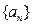 的前
的前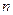 项和记作
项和记作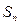 ,满足
,满足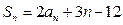 ,
,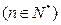 .
.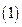 求出数列
求出数列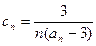 ,且
,且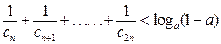 对正整数
对正整数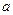 的范围;
的范围; 证明:
证明: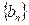 中不可能有等差子数列(已知
中不可能有等差子数列(已知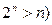 。
。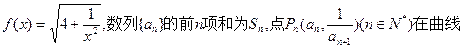
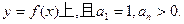
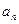 }的通项公式
}的通项公式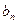 }的首项b1=1,前n项和为Tn,且
}的首项b1=1,前n项和为Tn,且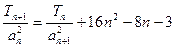 ,求数列{
,求数列{ 将M中的元素按从大到小的顺序排列,则第2005个数是( )
将M中的元素按从大到小的顺序排列,则第2005个数是( )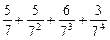
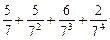
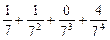
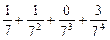
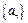
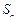


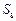

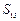
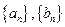
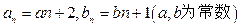
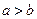
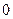 个
个 个
个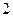 个
个