Question

【题目】点O为坐标原点，直线l经过抛物线C：y2=4x的焦点F．
（Ⅰ）若点O到直线l的距离为 ， 求直线l的方程；
（Ⅱ）设点A是直线l与抛物线C在第一象限的交点．点B是以点F为圆心，|FA|为半径的圆与x轴负半轴的交点．试判断直线AB与抛物线C的位置关系，并给出证明．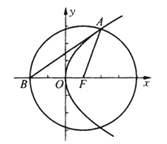

Answer 1

【答案】解法一：（Ⅰ）抛物线的焦点F（1，0），
当直线l的斜率不存在时，即x=1不符合题意．
当直线l的斜率存在时，
设直线l的方程为：y=k（x﹣1），即kx﹣y﹣k=0．
所以，，解得：．
故直线l的方程为：y=(x-1)，即
（Ⅱ）直线AB与抛物线相切，证明如下：
（法一）：设A（x0 ， y0），则．
因为|BF|=|AF|=x0+1，所以B（﹣x0 ， 0）．
所以直线AB的方程为：y=，
整理得：x=…（1）
把方程（1）代入y2=4x得：，
，
所以直线AB与抛物线相切．
【解析】（Ⅰ）抛物线的焦点F（1，0），当直线l的斜率不存在时，即x=1不符合题意．当直线l的斜率存在时，设直线l的方程为：y=k（x﹣1），所以 ， 由此能求出直线l的方程．
（Ⅱ）直线AB与抛物线相切．设A（x0 ， y0），则 ． 因为|BF|=|AF|=x0+1，所以B（﹣x0 ， 0），由此能够证明直线AB与抛物线相切．