题目内容
【题目】设函数
（
为常数，
是自然对数的底数）.
（Ⅰ）当
时，求函数
的单调区间；
（Ⅱ）若函数在
内存在两个极值点，求的取值范围.
【答案】（1）单调递减区间为
单调递增区间为
.（2）
【解析】分析：（Ⅰ）求出
，在定义域内，分别令
求得
的范围，可得函数
增区间，
求得的范围，可得函数的减区间；（Ⅱ）函数
在
内存在两个极值点，等价于它的导函数在内存内有两个不同的零点. 分三种情况讨论，分别利用导数研究函数的单调性，结合函数图，利用两点存在定理列不等式组，从而可得符合题意的
的取值范围.
详解：（Ⅰ）的定义域为
，
当
时，
，
令
则
当
时，
单调递减；
当
单调递增，
的单调递减区间为
单调递增区间为.
(Ⅱ）由（Ⅰ）知，时，函数在
内单调递减，
故在内不存在极值点；
当
，设函数
.
，
当
时，
当
时，
，
单调递增，
故故在内不存在两个极值点；
当
时，
得
时，
，函数单调递减，
时，
，函数单调递增，
函数的最小值为
函数在内存在两个极值点
当且仅当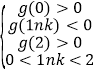
解得：
综上所述，函数在内存在两个极值点时，的取值范围为.
仁爱英语同步练习册系列答案
学习实践园地系列答案
【题目】已知函数f（x）=|x﹣a|，其中a＞1
（1）当a=2时，求不等式f（x）≥4﹣|x﹣4|的解集；
（2）已知关于x的不等式|f（2x+a）﹣2f（x）|≤2的解集{x|1≤x≤2}，求a的值．
【题目】某中学在校就餐的高一年级学生有440名，高二年级学生有460名，高三年级学生有500名；为了解学校食堂的服务质量情况，用分层抽样的方法从中抽取70名学生进行抽样调查，把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级：1级（很不满意）；2级（不满意）；3级（一般）；4级（满意）；5级（很满意），其统计结果如下表（服务满意度为x，价格满意度为y）．
y | 价格满意度 | |||||
1 | 2 | 3 | 4 | 5 | ||
服 | 1 | 1 | 1 | 2 | 2 | 0 |
2 | 2 | 1 | 3 | 4 | 1 | |
3 | 3 | 7 | 8 | 8 | 4 | |
4 | 1 | 4 | 6 | 4 | 1 | |
5 | 0 | 1 | 2 | 3 | 1 | |
（1）求高二年级共抽取学生人数；
（2）求“服务满意度”为3时的5个“价格满意度”数据的方差；
（3）为提高食堂服务质量，现从x＜3且2≤y＜4的所有学生中随机抽取两人征求意见，求至少有一人的“服务满意度”为1的概率．
