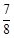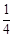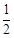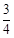题目内容
已知k∈(-1,2],则k的值使得过A(1,1)可以作两条直线与圆x2+y2+kx-2y-
k=0相切的概率等于 ( )
k=0相切的概率等于 ( )A． | B． | C． | D．不确定 |
B
∵圆的方程可化为(x+
)2+(y-1)2=
+
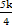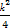+1,∴5k+k2+4>0,∴k<-4或k>-1.
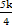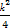∵过A(1,1)可以作两条直线与圆(x+)2+(y-1)2=++1相切,
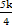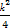∴A(1,1)在圆外,得(1+)2+(1-1)2>++1,
∴k<0,故符合条件的k∈(-1,0),其区间长度为1,因为k∈(-1,2],其区间长度为3,所以P=.
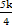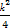)2+(y-1)2=++1,∴5k+k2+4>0,∴k<-4或k>-1.∵过A(1,1)可以作两条直线与圆(x+
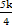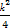)2+(y-1)2=++1相切,∴A(1,1)在圆外,得(1+
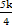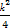)2+(1-1)2>++1,∴k<0,故符合条件的k∈(-1,0),其区间长度为1,因为k∈(-1,2],其区间长度为3,所以P=
.
练习册系列答案
相关题目
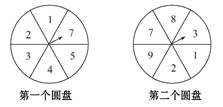
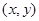，则点M取自阴影部分的概率为（ ）
+
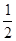
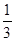
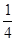
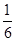
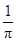
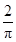
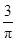
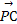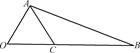
+2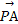
=0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
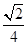
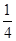
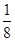
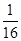
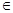（0,1），函数f（x）=x2+x+n有零点的概率为（ ）
