题目内容
8.若$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{BP}$,$\overrightarrow{AB}$=t$\overrightarrow{BP}$,则t的值是$-\frac{2}{3}$.分析 由题意得到A,B,P三点共线,并且BP=3AP,得到$\overrightarrow{AB}$,$\overrightarrow{BP}$的关系.
解答 解:由题意,$\overrightarrow{AP}$=$\frac{1}{3}$$\overrightarrow{BP}$,得到如图P,A,B的位置关系,所以$\overrightarrow{AB}=-\frac{2}{3}\overrightarrow{BP}$,所以t= $-\frac{2}{3}$;
$-\frac{2}{3}$;
故答案为:-$\frac{2}{3}$.
点评 本题考查了向量数乘、向量共线;属于基础题.

练习册系列答案
相关题目
19.已知向量$\overrightarrow{a}$=(x-5,3),$\overrightarrow{b}$=(2,x)且$\overrightarrow{a}$∥$\overrightarrow{b}$,则x的值为( )
| A. | 2或3 | B. | -1或6 | C. | 2 | D. | 6 |
3.设一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上10,得到一组新数据,则所得新数据的平均数和方差分别是( )
| A. | 13.6,12.8 | B. | 2.8,13.6 | C. | 12.8,13.6 | D. | 12.8,3.6 |
18.已知数列{an}中,a2=3,a4=15,若{an+1}为等比数列,则a6等于( )
| A. | 63 | B. | 64 | C. | 75 | D. | 65 |
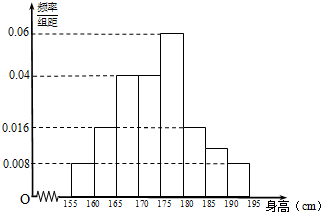 从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如.
从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如.