题目内容
16.已知向量$\vec a=({\sqrt{3}sinx,1})$,$\vec b=({cosx,{{sin}^2}x})$,函数$f(x)=\vec a•\vec b-\frac{1}{2}$.(1)求函数f(x)的最小正周期T;
(2)已知$f({\frac{α}{2}})=\frac{{\sqrt{5}}}{5}$,$f({\frac{β}{2}})=\frac{{3\sqrt{10}}}{10}$,$α∈({0,\frac{π}{2}})$,$β∈({0,\frac{π}{2}})$,求cos(α-β).
分析 (1)根据向量数量积的定义求出函数f(x)的表达式,即可求函数f(x)的最小正周期T;
(2)根据两角和差的余弦公式进行求解即可.
解答 解:(1)$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}=\sqrt{3}sinxcosx+{sin^2}x-\frac{1}{2}$
=$\frac{{\sqrt{3}}}{2}sin2x+\frac{1-cos2x}{2}-\frac{1}{2}=\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x$=$sin(2x-\frac{π}{6})$,
故函数f(x)的最小正周期T=π.
(2)由$f(\frac{α}{2})=\frac{{\sqrt{5}}}{5}$,$f(\frac{β}{2})=\frac{{3\sqrt{10}}}{10}$,
得:$sin(α-\frac{π}{6})=\frac{{\sqrt{5}}}{5}$,$sin(β-\frac{π}{6})=\frac{{3\sqrt{10}}}{10}$
又$α∈(0,\frac{π}{2})$,$β∈(0,\frac{π}{2})$
∴$α-\frac{π}{6}∈(-\frac{π}{6},\frac{π}{3})$,$β-\frac{π}{6}∈(-\frac{π}{6},\frac{π}{3})$
∴$cos(α-\frac{π}{6})=\frac{{2\sqrt{5}}}{5}$,$cos(β-\frac{π}{6})=\frac{{\sqrt{10}}}{10}$.
∴$cos(α-β)=cos[(α-\frac{π}{6})-(β-\frac{π}{6})]$
$\begin{array}{l}=cos(α-\frac{π}{6})cos(β-\frac{π}{6})+sin(α-\frac{π}{6})sin(β-\frac{π}{6})\\=\frac{{2\sqrt{5}}}{5}×\frac{{\sqrt{10}}}{10}+\frac{{\sqrt{5}}}{5}×\frac{{3\sqrt{10}}}{10}\end{array}$
=$\frac{{\sqrt{2}}}{2}$.
点评 本题主要考查三角函数周期的计算,以及三角函数值的化简和求解,利用两角和差的余弦公式是解决本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 2i | B. | -2i | C. | 2 | D. | -2 |
| A. | 不等边三角形 | B. | 钝角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
| A. | 5,15,25,36,45,55 | B. | 2,4,8,16,32,48 | ||
| C. | 2,12,23,34,45,56 | D. | 3,13,23,33,43,53 |
| A. | ${a_n}=\frac{{3+{{(-1)}^n}}}{2}$ | B. | ${a_n}=\frac{{3+{{(-1)}^{n+1}}}}{2}$ | ||
| C. | ${a_n}=\frac{3+cosnπ}{2}$ | D. | ${a_n}=\frac{{3+sin\frac{2n+1}{2}π}}{2}$ |
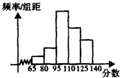 为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.
为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.