题目内容
P是双曲线x2-y2=16的左支上一点，F1、F2分别是左、右焦点，则|PF1|-|PF2|=_________.
-8
由x2-y2=16知a=4.
又∵P在双曲线x2-y2=16的左支上,
∴|PF1|-|PF2|=-2a=-8,
即|PF1|-|PF2|=-8.
又∵P在双曲线x2-y2=16的左支上,
∴|PF1|-|PF2|=-2a=-8,
即|PF1|-|PF2|=-8.
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
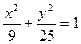共焦点，它们的离心率之和为
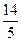，求双曲线方程.(10分) 
-
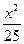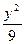=1上的一点，且|PF1|=12,则|PF2|等于( )
-
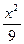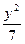="1(x>3) " B.
-
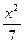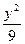=1(x<-7)
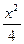-y2=1.
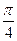,被双曲线截得的弦长为
，求直线l的方程;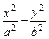
=1的右焦点是F，右顶点是A,虚轴的上端点是B，
·
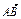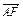=6-4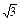
，∠BAF=150°.
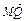+2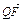
=0，求直线l的斜率.