题目内容
双曲线的方程是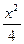 -y2=1.
-y2=1.
(1)直线l的倾斜角为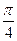 ,被双曲线截得的弦长为
,被双曲线截得的弦长为
 ,求直线l的方程;
,求直线l的方程;
(2)过点P(3,1)作直线l′,使其截得的弦恰被P点平分,求直线l′的方程.
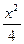 -y2=1.
-y2=1.(1)直线l的倾斜角为
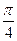 ,被双曲线截得的弦长为
,被双曲线截得的弦长为
 ,求直线l的方程;
,求直线l的方程;(2)过点P(3,1)作直线l′,使其截得的弦恰被P点平分,求直线l′的方程.
1、y=x±5.
2、所求直线l′的方程为3x-4y-5=0.
2、所求直线l′的方程为3x-4y-5=0.
(1)设直线l的方程为y=x+m,代入双曲线方程,得
3x2+8mx+4(m2+1)=0,Δ=(8m)2-4×3×4(m2+1)=16(m2-3)>0,
∵m2>3.
设直线l与双曲线交于A(x1,y1)、B(x2,y2)两点,
则x1+x2=- m,x1x2=
m,x1x2=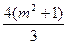 ,由弦长公式|AB|=
,由弦长公式|AB|=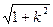 |x1-x2|得
|x1-x2|得
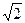 ·
·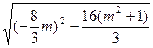 =
=
 ,∴
,∴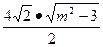 =
=
 ,即m=±5,∴直线l的方程为y=x±5.
,即m=±5,∴直线l的方程为y=x±5.
(2)设与双曲线交于A′(x1,y1)、B′(x2,y2)两点.点P(3,1)为A′、B′的中点,则x1+x2=6,y1+y2=2.由x12-4y12=4,x22-4y22=4,两式相减得(x1+x2)(x1-x2)-4(y1+y2)(y1-y2)=0,∴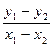 =
=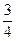 ,∴l′的方程为y-1=
,∴l′的方程为y-1=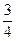 (x-3),即3x-4y-5=0.把此方程代入双曲线方程,整理得5y2+10y+
(x-3),即3x-4y-5=0.把此方程代入双曲线方程,整理得5y2+10y+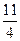 =0,∵Δ>0,∴所求直线与双曲线有两个交点,即所求直线l′的方程为3x-4y-5=0.
=0,∵Δ>0,∴所求直线与双曲线有两个交点,即所求直线l′的方程为3x-4y-5=0.
3x2+8mx+4(m2+1)=0,Δ=(8m)2-4×3×4(m2+1)=16(m2-3)>0,
∵m2>3.
设直线l与双曲线交于A(x1,y1)、B(x2,y2)两点,
则x1+x2=-
 m,x1x2=
m,x1x2=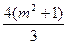 ,由弦长公式|AB|=
,由弦长公式|AB|=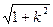 |x1-x2|得
|x1-x2|得 ·
·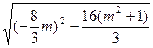 =
=
 ,∴
,∴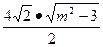 =
=
 ,即m=±5,∴直线l的方程为y=x±5.
,即m=±5,∴直线l的方程为y=x±5.(2)设与双曲线交于A′(x1,y1)、B′(x2,y2)两点.点P(3,1)为A′、B′的中点,则x1+x2=6,y1+y2=2.由x12-4y12=4,x22-4y22=4,两式相减得(x1+x2)(x1-x2)-4(y1+y2)(y1-y2)=0,∴
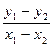 =
=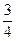 ,∴l′的方程为y-1=
,∴l′的方程为y-1=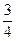 (x-3),即3x-4y-5=0.把此方程代入双曲线方程,整理得5y2+10y+
(x-3),即3x-4y-5=0.把此方程代入双曲线方程,整理得5y2+10y+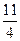 =0,∵Δ>0,∴所求直线与双曲线有两个交点,即所求直线l′的方程为3x-4y-5=0.
=0,∵Δ>0,∴所求直线与双曲线有两个交点,即所求直线l′的方程为3x-4y-5=0.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
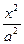 -
- =1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于___________.
=1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于___________.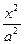 -
-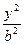 =1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )
=1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )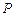 的轨迹是曲线
的轨迹是曲线 ,满足点
,满足点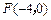 的距离与它到直线
的距离与它到直线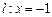 的距离
的距离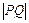 之比为常数,又点
之比为常数,又点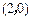 在曲线
在曲线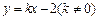 与曲线
与曲线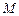 和
和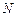 ,求实数
,求实数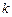 的取值范围.
的取值范围.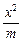 +
+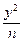 =1(m>n>0)和双曲线
=1(m>n>0)和双曲线 -
-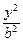 =1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是
=1(a>b>0)有相同的焦点F1、F2,P是两条曲线的一个交点,则|PF1|·|PF2|的值是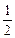 (m-a)
(m-a)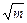 -
-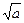
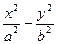 =1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )
=1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )