题目内容
7．已知A（3，0），B（4，4），C（2，1），求AC和OB的交点P的坐标．分析 由题意可得直线的斜率，进而可得直线的方程，联立解方程组可得．
解答 解：由题意可得AC的斜率kAC=$\frac{0-1}{3-2}$=-1，
∴直线AC的方程为y-0=-（x-3）即y=3-x；
同理可得OB的斜率kOB=$\frac{4-0}{4-0}$=1，
∴直线OB的方程为y-0=（x-0）即y=x，
联立方程组可得$\left\{\begin{array}{l}{y=3-x}\\{y=x}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{3}{2}}\end{array}\right.$，
∴AC和OB的交点P的坐标为（$\frac{3}{2}$，$\frac{3}{2}$）
点评 本题考查直线的交点坐标，涉及直线方程的求解，属基础题．
练习册系列答案
相关题目
2．已知集合A={x|x2=2}，B={1，$\sqrt{2}$，2}，则A∩B=（ ）
| A． | {2} | B． | {$\sqrt{2}$} | C． | {-$\sqrt{2}$，1，$\sqrt{2}$，2} | D． | {1，$\sqrt{2}$，2} |
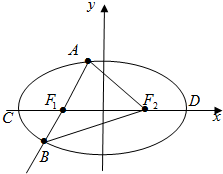椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点为F1、F2，离心率为$\frac{1}{2}$，过点F1的直线l交椭圆于A、B两点，△AF2B的周长为8．