题目内容
15.棱长为1的正方体ABCD-A1B1C1D1中,点M,N,P分别为AB1,BC1,DD1的中点,给出下列结论:①MN⊥AA1
②直线C1M与平面ABCD所成角的正弦值为$\frac{{\sqrt{5}}}{5}$
③MN⊥BP
④四面体B-DA1C1的体积为$\frac{1}{3}$
则正确结论的序号为①②③④.
分析 如图所示,建立空间直角坐标系.A(1,0,0),A1(1,0,1),M$(1,\frac{1}{2},\frac{1}{2})$,N$(\frac{1}{2},1,\frac{1}{2})$,C1(0,1,1),B(1,1,0),P$(0,0,\frac{1}{2})$.
①只要计算$\overrightarrow{MN}•\overrightarrow{A{A}_{1}}$=0是否成立,即可判断出正误;
②取平面ABCD的法向量$\overrightarrow{n}$=(0,0,1),设直线C1M与平面ABCD所成角为θ,利用sinθ=$|cos<\overrightarrow{M{C}_{1}},\overrightarrow{n}>|$=$\frac{|\overrightarrow{M{C}_{1}}•\overrightarrow{n}|}{|\overrightarrow{M{C}_{1}}||\overrightarrow{n}|}$,即可判断出正误;
③只要计算$\overrightarrow{MN}•\overrightarrow{BP}$=0是否成立,即可判断出正误;
④${V}_{B-D{A}_{1}{C}_{1}}$=${V}_{正方体A{C}_{1}}$-4×${V}_{三棱锥{A}_{1}-ABD}$,即可判断出正误.
解答 解:如图所示,建立空间直角坐标系.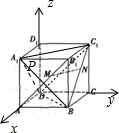
A(1,0,0),A1(1,0,1),M$(1,\frac{1}{2},\frac{1}{2})$,N$(\frac{1}{2},1,\frac{1}{2})$,C1(0,1,1),B(1,1,0),P$(0,0,\frac{1}{2})$.
①$\overrightarrow{MN}$=$(-\frac{1}{2},\frac{1}{2},0)$,$\overrightarrow{A{A}_{1}}$=(0,0,1),∴$\overrightarrow{MN}•\overrightarrow{A{A}_{1}}$=0,∴$\overrightarrow{MN}⊥\overrightarrow{A{A}_{1}}$,∴MN⊥AA1,正确;
②$\overrightarrow{M{C}_{1}}$=$(-1,\frac{1}{2},\frac{1}{2})$,取平面ABCD的法向量$\overrightarrow{n}$=(0,0,1),设直线C1M与平面ABCD所成角为θ,
则sinθ=$|cos<\overrightarrow{M{C}_{1}},\overrightarrow{n}>|$=$\frac{|\overrightarrow{M{C}_{1}}•\overrightarrow{n}|}{|\overrightarrow{M{C}_{1}}||\overrightarrow{n}|}$=$\frac{\frac{1}{2}}{\sqrt{{1}^{2}+(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}×1}$=$\frac{\sqrt{5}}{5}$,正确;
③$\overrightarrow{BP}$=$(-1,-1,\frac{1}{2})$,∴$\overrightarrow{MN}•\overrightarrow{BP}$=$\frac{1}{2}-\frac{1}{2}+0$=0,∴$\overrightarrow{MN}⊥\overrightarrow{BP}$,∴MN⊥BP,正确;
④${V}_{B-D{A}_{1}{C}_{1}}$=${V}_{正方体A{C}_{1}}$-4×${V}_{三棱锥{A}_{1}-ABD}$=${1}^{3}-4×\frac{1}{3}×\frac{1}{2}×{1}^{2}×1$=$\frac{1}{3}$,因此正确.
综上可得:①②③④都正确.
故答案为:①②③④.
点评 本题考查了利用向量垂直与数量积的关系、线面角的计算公式、三棱锥的体积计算公式,考查了空间想象能力、推理能力与计算能力,属于中档题.

| A. | 2+$\frac{1}{2}$log32 | B. | 2-$\frac{1}{2}$log23 | C. | 2+log23 | D. | 2+$\frac{1}{3}$log23 |
| A. | $\frac{5}{6}$ | B. | $\frac{3}{13}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
| A. | f(x)=x,g(x)=(x${\;}^{\frac{1}{2}}$)2 | B. | f(x)=$\sqrt{1-{x}^{2}}$,g(x)=1-|x|,x∈[-1,1] | ||
| C. | y=f(x),g(x)=f(x+1),x∈R | D. | f(x)=|lg0.5x|,g(x)=|x|lg2 |
 如图,已知椭圆C$\frac{{x}^{2}}{2}+{y}^{2}=1$,点B坐标为(0,-1),过点B的直线与椭圆C的另外一个交点为A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C$\frac{{x}^{2}}{2}+{y}^{2}=1$,点B坐标为(0,-1),过点B的直线与椭圆C的另外一个交点为A,且线段AB的中点E在直线y=x上.