题目内容
2.如图,四棱锥P-ABCD的底面为矩形,AB=$\sqrt{2}$,BC=1,E,F分别是AB,PC的中点,DE⊥PA,求证:平面PAC⊥平面PDE.
分析 根据面面垂直的判定定理,只要证明DE⊥平面PAC,再证明平面PAC⊥平面PDE.
解答 证明:设AC∩DE=G,由△AEG∽△CDG及E为AB中点得$\frac{AG}{CG}=\frac{AE}{CD}=\frac{1}{2}$,
又因为AB=$\sqrt{2}$,BC=1,所以AC=$\sqrt{3}$,AG=$\frac{1}{3}$AC=$\frac{\sqrt{3}}{3}$.
所以$\frac{AG}{AE}=\frac{AB}{AC}=\frac{\sqrt{2}}{\sqrt{3}}$,
又∠BAC为公共角,所以△GAE∽△BAC.
所以∠AGE=∠ABC=90°,即DE⊥AC.
又DE⊥PA,PA∩AC=A,
所以DE⊥平面PAC.
又DE?平面PDE,
所以平面PAC⊥面PDE.
点评 本题以四棱锥为例,考查了空间的平面与平面垂直的判定,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.
将正偶数列{2n}中的所有项按每一行比上一行多一项的规则排成如图数表:记aij是这个数表的第i行第j列的数.例如a43=18.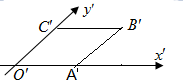 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )