题目内容
5.在区间[-6,6]内任取一个元素x0,若抛物线x2=2y在x=x0处的切线的斜率为k,则k∈[-1,1]的概率为1616.分析 由切线斜率的范围,由导数的几何意义求出x0的范围,进而求出x0所在区间的长度,最后得出答案.
解答 解:由k∈[-1,1],
x2=2y,则 y′=x,
所以-1≤x0≤1,
∴[-6,6]∩[-1,1]=[-1,1],
∴点x0所在区间的长度=2,区间[-6,6]的长度=12,
所以P=212212=1616.
故答案为:1616.
点评 本题考查导数的几何意义和几何概型的应用,正确理解题意是解题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
20.某程序框图如图所示,则输出的结果为( )
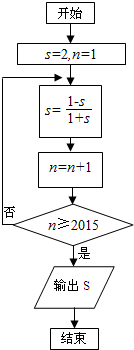

| A. | 1212 | B. | 2 | C. | -1313 | D. | -3 |
10.已知向量→m→m=(1,1),→n→n与→m→m的夹角为3π43π4,且→m→m•→n→n=-1,则向量→n→n=( )
| A. | (-1,0) | B. | (0,-1) | C. | (-1,0)或(0,-1) | D. | (-1,-1) |
14.已知|→a→a|=4,|→b→b|=8,→a→a与→b→b夹角是120°.
(1)求→a•→b→a∙→b的值及|→a+→b→a+→b|的值;
(2)当k为何值时,(→a+2→b)⊥(k→a−→b)?
(1)求→a•→b→a∙→b的值及|→a+→b→a+→b|的值;
(2)当k为何值时,(→a+2→b)⊥(k→a−→b)?
15.复数2i1+i=( )
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |