题目内容
已知函数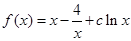 ,其中
,其中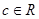 ,
,
(1)当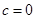 时,求曲线
时,求曲线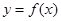 在点
在点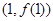 处的切线方程;
处的切线方程;
(2)讨论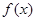 的单调性;
的单调性;
(3)若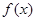 有两个极值点
有两个极值点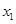 和
和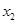 ,记过点
,记过点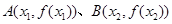 的直线的斜率为
的直线的斜率为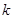 ,问是否存在
,问是否存在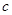 ,使得
,使得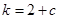 ?若存在,求出
?若存在,求出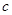 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
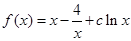 ,其中
,其中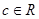 ,
,(1)当
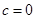 时,求曲线
时,求曲线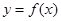 在点
在点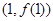 处的切线方程;
处的切线方程;(2)讨论
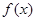 的单调性;
的单调性;(3)若
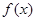 有两个极值点
有两个极值点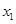 和
和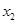 ,记过点
,记过点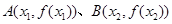 的直线的斜率为
的直线的斜率为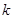 ,问是否存在
,问是否存在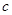 ,使得
,使得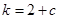 ?若存在,求出
?若存在,求出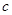 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.(1)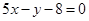 ;(2)
;(2)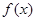 分别在
分别在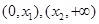 上单调递增,在
上单调递增,在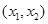 上单调递减;(3)不存在
上单调递减;(3)不存在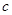 ,使得
,使得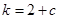 .
.
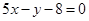 ;(2)
;(2)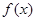 分别在
分别在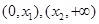 上单调递增,在
上单调递增,在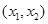 上单调递减;(3)不存在
上单调递减;(3)不存在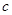 ,使得
,使得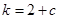 .
.试题分析:(1)当
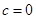 时,
时,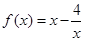 ,那么曲线
,那么曲线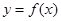 在点
在点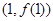 处的切线的斜率
处的切线的斜率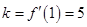 ,根据点斜式写出直线的方程为
,根据点斜式写出直线的方程为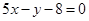 ;(2)函数
;(2)函数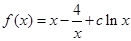 求导得
求导得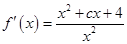 ,
,由于函数
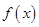 的定义域是
的定义域是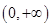 ,因此只需要讨论分子在
,因此只需要讨论分子在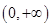 上的正负问题;(3)假设存在
上的正负问题;(3)假设存在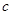 ,使得
,使得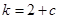 ,那么计算出
,那么计算出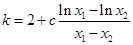 ,问题归结为
,问题归结为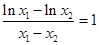 是否成立,可设函数
是否成立,可设函数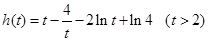 ,
,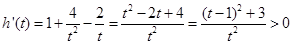 ,所以
,所以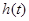 在
在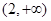 上单调递增,因此不存在
上单调递增,因此不存在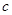 ,使得
,使得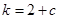 .
.试题解析:(1)当
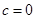 时,
时,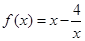 ,所以
,所以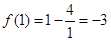
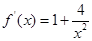 ,
, 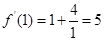 ,
, 又因为切线过
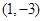 ,所以切线方程为
,所以切线方程为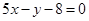
(2)
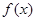 的定义域为
的定义域为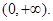
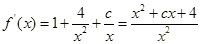 ,
,令
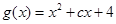 ,其判别式
,其判别式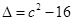
①当
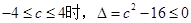 ,故
,故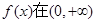 上单调递增
上单调递增② 当
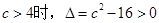 ,
,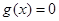 的两根都小于0,在
的两根都小于0,在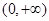 上,
上,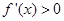 ,故
,故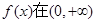 上单调递增.
上单调递增. ③当
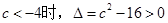 ,设
,设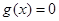 的两根为,
的两根为,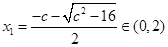
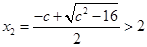
当
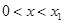 时,
时, 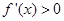 ;当
;当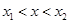 时,
时, 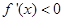 ;当
;当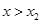 时,
时, 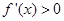 ,故
,故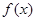 分别在
分别在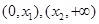 上单调递增,在
上单调递增,在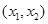 上单调递减.
上单调递减. (3)由(2)可知:当
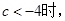
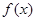 在
在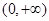 上有两个极值点
上有两个极值点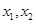
因为
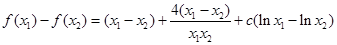
所以
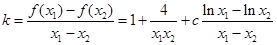
由(2)可知:
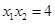 ,于是
,于是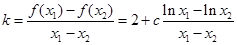 ,
,若存在
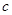 ,使得
,使得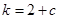 ,则
,则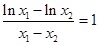 ,即
,即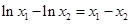 ,
,亦即
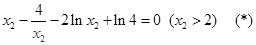
设函数
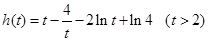 ,
,当
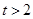 时,
时,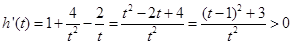 ,所以
,所以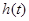 在
在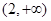 上单调递增,
上单调递增, 而
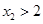 ,所以
,所以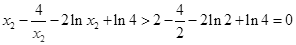 ,
,这与
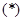 式矛盾.故不存在
式矛盾.故不存在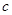 ,使得
,使得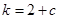

练习册系列答案
相关题目
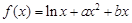 (其中
(其中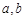 为常数且
为常数且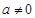 )在
)在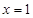 处取得极值.
处取得极值. 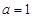 时,求
时,求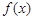 的单调区间;
的单调区间;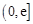 上的最大值为
上的最大值为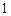 ,求
,求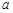 的值.
的值.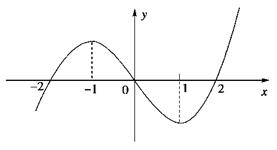
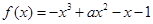 在
在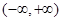 上是单调减函数,则实数
上是单调减函数,则实数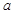 的取值范围是___________.
的取值范围是___________.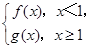 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.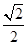 ,
,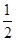 ),则函数g(x)=
),则函数g(x)=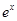 f(x)的单调递减区间为( )
f(x)的单调递减区间为( )