题目内容
4.已知函数f(x)=|x-10|+|x-20|,且满足f(x)<10a(a∈R)的解集不是空集.(Ⅰ)求实数a的取值范围;
(Ⅱ)求a+$\frac{4}{{a}^{2}}$的最小值.
分析 (Ⅰ)由条件利用绝对值的意义求得函数f(x)<10a的解集不是空集时,a的范围.
(Ⅱ)由条件利用基本不等式求得a+$\frac{4}{{a}^{2}}$的最小值
解答 解:(Ⅰ)函数f(x)=|x-10|+|x-20|表示数轴上的x对应点到10、20对应点的距离之和,
它的最小值为10,由f(x)<10a(a∈R)的解集不是空集,可得10a>10,a>1.
(Ⅱ)当a>1时,$a+\frac{4}{a^2}=\frac{a}{2}+\frac{a}{2}+\frac{4}{a^2}$,
又 $\frac{a}{2}+\frac{a}{2}+\frac{4}{a^2}≥3\root{3}{{\frac{a}{2}•\frac{a}{2}•\frac{4}{a^2}}}=3$,当且仅当$\frac{a}{2}=\frac{4}{a^2}$,即a=2时等号成立,
所以$a+\frac{4}{a^2}$的最小值为3.
点评 本题主要考查绝对值的意义,基本不等式的应用,属于基础题.

练习册系列答案
相关题目
19.各项都是正数的等比数列{an},若a2,$\frac{1}{2}$a3,2a1成等差数列,则$\frac{{a}_{3}+{a}_{4}}{{a}_{4}+{a}_{5}}$的值为( )
| A. | 2 | B. | 2或-1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$或-1 |
9.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
| A. | ∠ADE=20° | B. | ∠ADE=30° | C. | ∠ADE=$\frac{1}{3}$∠ADC | D. | ∠ADE=$\frac{1}{2}$∠ADC |
14.命题p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6相交.则?p及?p的真假为( )
| A. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为真 | |
| B. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为假 | |
| C. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为真 | |
| D. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为假 |
 如图,在正方体ABCD-A1B1C1D1中,体对角线A1C与面对角线DB异面且垂直.
如图,在正方体ABCD-A1B1C1D1中,体对角线A1C与面对角线DB异面且垂直.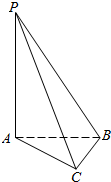 如图,在Rt△ABC中,AC=BC,PA⊥平面ABC,PB与平面ABC成60°角
如图,在Rt△ABC中,AC=BC,PA⊥平面ABC,PB与平面ABC成60°角