题目内容
9．在四边形ABCD中，∠A=∠B=∠C，点E在边AB上，∠AED=60°，则一定有（ ）| A． | ∠ADE=20° | B． | ∠ADE=30° | C． | ∠ADE=$\frac{1}{3}$∠ADC | D． | ∠ADE=$\frac{1}{2}$∠ADC |
分析 由∠AED=60°，求得∠BED的度数，利用四边形的内角和为360°，求出∠B的度数，即可得到∠A，再根据三角形的内角和为180°，即可解答．
解答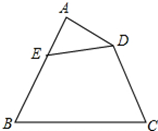 
解：∵∠AED=60°，
∴∠BED=180°-∠AED=180°-60°=120°，
∴∠B+∠C=360°-∠BED-∠EDC=360°-120°-100°=140°，
∵∠B=∠C，
∴∠B=∠C=70°，
∴∠A=70°，∠EDC=100°
∴∠ADE=180°-∠A-∠AED=180°-70°-60°=50°，
∴∠ADE=$\frac{1}{3}$∠ADC
故选：C．
点评 本题考查了多边形的内角和，解决本题的关键是熟记四边形的内角和为360°．
练习册系列答案
备战中考寒假系列答案
相关题目
17．设y1=40.9，y2=log${\;}_{\frac{1}{2}}$4.3，y3=（$\frac{1}{3}$）1.5，则（ ）
| A． | y3＞y1＞y2 | B． | y2＞y1＞y3 | C． | y1＞y2＞y3 | D． | y1＞y3＞y2 |
14．在正方体ABCD-A1B1C1D1中，下列几种说法不正确的是（ ）
| A． | A1C1⊥BD | B． | D1C1∥AB | ||
| C． | 二面角A1-BC-D的平面角为45° | D． | AC1与平面ABCD所成的角为45° |
18．在平行四边形ABCD中，M为对角线AC上一点，且$\overrightarrow{{A}{M}}=\frac{1}{3}\overrightarrow{{A}C}$，设$\overrightarrow{{A}{B}}=\vec a$，$\overrightarrow{{A}D}=\vec b$，则$\overrightarrow{{M}{A}}+\overrightarrow{{M}{B}}$=（ ）
| A． | $\frac{1}{3}\vec a+\frac{1}{3}\vec b$ | B． | $\frac{1}{3}\vec a+\frac{2}{3}\vec b$ | C． | $\frac{1}{3}\vec a-\frac{2}{3}\vec b$ | D． | $\frac{1}{3}\vec a-\frac{1}{3}\vec b$ |