题目内容
【题目】如图,平面![]() 平面
平面![]() ,其中
,其中![]() 为矩形,
为矩形,![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求
,求![]() 的长.
的长.

【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)由条件易得![]() 和
和![]() ,从而可证得
,从而可证得![]() 平面
平面![]() ;
;
(Ⅱ)设AB=x.以F为原点,AF,FE所在的直线分别为x轴,y轴建立空间直角坐标系,平面ABF的法向量可取![]() =(0,1,0),通过求解平面BFD的法向量
=(0,1,0),通过求解平面BFD的法向量![]() ,进而利用法向量求二面角的余弦值列方程求解即可.
,进而利用法向量求二面角的余弦值列方程求解即可.
(Ⅰ)![]() 平面
平面![]() 平面
平面![]() ,且
,且![]() 为矩形,
为矩形,
![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]()
![]() ,又
,又![]() 且
且![]()
![]() 平面
平面![]() .
.
(Ⅱ)设AB=x.以F为原点,AF,FE所在的直线分别为x轴,y轴建立空间直角坐标系![]() .
.
则F(0,0,0),A(-2,0,0),E(0,![]() ,0),D(-1,
,0),D(-1,![]() ,0),B(-2,0,x),
,0),B(-2,0,x),
所以![]() =(1,-
=(1,-![]() ,0),
,0),![]() =(2,0,-x).
=(2,0,-x).
因为EF⊥平面ABF,所以平面ABF的法向量可取![]() =(0,1,0).
=(0,1,0).
设![]() =(x1,y1,z1)为平面BFD的法向量,
=(x1,y1,z1)为平面BFD的法向量,
则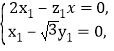 所以,可取
所以,可取![]() =(
=(![]() ,1,
,1,![]() ).
).
因为cos<![]() ,
,![]() >=
>=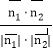 =
=![]() ,得x=
,得x=![]() ,所以AB=
,所以AB=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】以下是某地搜集到的新房屋的销售价格![]() 和房屋的面积
和房屋的面积![]() 的数据:
的数据:
房屋面积( | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150![]() 时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]()
【题目】为推行“新课堂”教学法,某化学老师分别用传统教学和“新课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验.为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
乙班频数 | 1 | 3 | 6 | 5 | 5 |
(1)由以上统计数据填写下面![]() 列联表,并判断能否在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
列联表,并判断能否在犯错概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附: ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中,记成绩不优良的乙班人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.

