题目内容
6.已知y=f(x)与y=f(x+1)都是定义在R上的偶函数,当x∈[-1,0]时,f(x)=-2x2-4x-2,若y=f(x)与g(x)=loga(x+1)的图象至少有3个交点,则a取值范围为( )| A. | 0<a<$\frac{\sqrt{3}}{3}$ | B. | 0<a<$\frac{\sqrt{6}}{6}$ | C. | 1<a<$\sqrt{3}$ | D. | 1<a<$\sqrt{6}$ |
分析 根据函数的奇偶性的性质判断函数的周期性,作出函数f(x)的图象,利用数形结合建立不等式关系即可得到结论.
解答 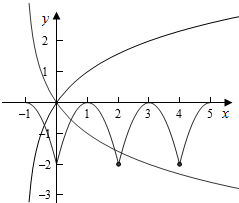 解:∵y=f(x)与y=f(x+1)都是定义在R上的偶函数,
解:∵y=f(x)与y=f(x+1)都是定义在R上的偶函数,
∴f(-x+1)=f(x+1),
即f(-x+1)=f(x+1)=f(x-1),
即f(x+2)=f(x),
则函数f(x)是周期为2的周期函数,
当x∈[0,1]时,-x∈[-1,0],
此时f(-x)=-2x2+4x-2=f(x),
即f(x)=-2x2+4x-2,x∈[0,1],
当x=2时,f(2)=f(0)=-2,
作出f(x)的图象如图:
当a>1时,f(x)与g(x)只有一个交点,不满足条件.
当0<a<1时,若y=f(x)与g(x)=loga(x+1)的图象至少有3个交点,
则满足g(2)>-2,
即loga(2+1)>-2,
即loga3>-2,
即loga3>-2logaa=logaa-2,
即a-2>3,
则a2<$\frac{1}{3}$,
解得0<a<$\frac{\sqrt{3}}{3}$,
故选:A
点评 本题主要考查函数与方程的应用,根据函数奇偶性的性质求出函数的解析式,作出函数的图象,利用数形结合是解决本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.已知向量$\overrightarrow{a}$=(2,4),$\overrightarrow{b}$=(-1,1),则2$\overrightarrow{a}$+$\overrightarrow{b}$等于( )
| A. | (5,7) | B. | (5,9) | C. | (3,7) | D. | (3,9) |