题目内容
4.在极坐标系中,已知直线l的极坐标方程为$ρsin(θ+\frac{π}{4})=1+\sqrt{2}$,圆C的圆心是$C(\sqrt{2},\frac{π}{4})$,半径为$\sqrt{2}$.(Ⅰ)求圆C的极坐标方程;
(Ⅱ)求直线l被圆C所截得的弦长.
分析 (Ⅰ)求出圆心坐标,和圆的标准方程,即可求圆C的极坐标方程;
(Ⅱ)分别求出直线的标准方程,利用直线和圆的位置关系即可求直线l被圆C所截得的弦长.
解答 解:(Ⅰ)∵圆C的圆心是$C(\sqrt{2},\frac{π}{4})$,
∴x=ρcosθ=$\sqrt{2}×\frac{\sqrt{2}}{2}$=1,y=ρsinθ=$\sqrt{2}×\frac{\sqrt{2}}{2}$=1,
即圆心坐标为(1,1),
则圆的标准方程为(x-1)2+(y-1)2=2,x2-2x+y2-2y=0
圆C的极坐标方程为:$ρ=2\sqrt{2}cos(θ-\frac{π}{4})$;
(Ⅱ)∵直线l的极坐标方程为$ρsin(θ+\frac{π}{4})=1+\sqrt{2}$,
∴$\frac{\sqrt{2}}{2}$ρsinθ+$\frac{\sqrt{2}}{2}$ρcosθ=1+$\sqrt{2}$,
即$x+y=2+\sqrt{2}$,
圆心到直线距离为$d=\frac{{|1+1-2-\sqrt{2}|}}{{\sqrt{2}}}=1$,圆半径为$\sqrt{2}$.
故弦长为$2\sqrt{{r^2}-{d^2}}=2$.
点评 本题主要考查参数方程和极坐标方程的应用,利用极坐标和直角坐标系之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知y=f(x)与y=f(x+1)都是定义在R上的偶函数,当x∈[-1,0]时,f(x)=-2x2-4x-2,若y=f(x)与g(x)=loga(x+1)的图象至少有3个交点,则a取值范围为( )
| A. | 0<a<$\frac{\sqrt{3}}{3}$ | B. | 0<a<$\frac{\sqrt{6}}{6}$ | C. | 1<a<$\sqrt{3}$ | D. | 1<a<$\sqrt{6}$ |
7.已知$\overrightarrow{a}$=($\sqrt{3}$,1),$\overrightarrow{b}$=(-3,$\sqrt{3}$),则<$\overrightarrow{a}$,$\overrightarrow{b}$>=( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
4.若log2a,log2b是方程x2+x-3=0的两根,则(lg$\frac{a}{b}$)2等于( )
| A. | 13 | B. | 13(lg2)2 | C. | 10 | D. | 10(lg2) |
16.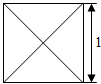 已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
 已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )
已知某几何体的俯视图是如图所示的边长为1的正方形,主视图与左视图是边长为1的正三角形,则其全面积是( )| A. | 2 | B. | 3 | C. | $1+\sqrt{3}$ | D. | $\sqrt{3}$ |
13.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
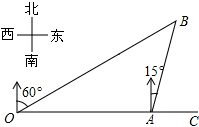

| A. | 4km | B. | 2$\sqrt{3}$km | C. | 2$\sqrt{2}$km | D. | ($\sqrt{3}$+1)km |
14.双曲线x2-y2=1右支上一点P(a,b)到直线l:y=x的距离d=$\sqrt{2}$.则a+b=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$或-$\frac{1}{2}$ | D. | 2或-2 |