题目内容
【题目】已知函数f(x)=1﹣ ![]() 在R上是奇函数.
在R上是奇函数.
(1)求a;
(2)对x∈(0,1],不等式sf(x)≥2x﹣1恒成立,求实数s的取值范围;
(3)令g(x)= ![]() ,若关于x的方程g(2x)﹣mg(x+1)=0有唯一实数解,求实数m的取值范围.
,若关于x的方程g(2x)﹣mg(x+1)=0有唯一实数解,求实数m的取值范围.
【答案】
(1)解:由题意知f(0)=0.即 ![]() ,
,
所以a=2.此时f(x)= ![]() ,
,
而f(﹣x)= ![]() ,
,
所以f(x)为奇函数,故a=2为所求
(2)解:由(1)知 ![]() ,
,
因为x∈(0,1],所以2x﹣1>0,2x+1>0,
故sf(x)≥2x﹣1恒成立等价于s≥2x+1恒成立,
因为2x+1∈(2,3],所以只需s≥3即可使原不等式恒成立.
故s的取值范围是[3,+∞)
(3)解:因为 ![]() .
.
所以g(2x)﹣mg(x+1)= ![]() .
.
整理得22x﹣2m2x﹣m+1=0.
令t=2x>0,则问题化为t2﹣2mt﹣m+1=0有一个正根或两个相等正根.
令h(t)=t2﹣2mt﹣m+1(t>0),则函数h(t)=t2﹣2mt﹣m+1在(0,+∞)上有唯一零点.
所以h(0)≤0或 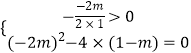 ,
,
由h(0)≤0得m≥1,
易知m=1时,h(t)=t2﹣2t符合题意;
由 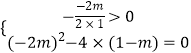 解得
解得 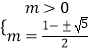 ,
,
所以m= ![]() .
.
综上m的取值范围是 ![]()
【解析】(1)根据f(0)=0可求得a的值,然后验证a的取值满足函数为奇函数;(2)分离参数法,将问题转化为函数的最值问题求解;(3)可先将方程化简,然后问题转化为一元二次方程在指定区间上根的分布问题,然后再进一步求解.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.