Question

【题目】设函数y=f（x）是定义在（0，+∞）上的函数，并且满足下面三个条件： ①对任意正数x，y，都有f（xy）=f（x）+f（y）；
②当x＞1时，f（x）＞0；
③f（3）=1，
（1）求f（1）， 的值；
（2）判断函数f（x）在区间（0，+∞）上单调性，并用定义给出证明；
（3）对于定义域内的任意实数x，f（kx）+f（4﹣x）＜2（k为常数，且k＞0）恒成立，求正实数k的取值范围．

Answer 1

【答案】
（1）解：令x=y=1，得f（1）=0，令x=3， ，

则 ，所以

（2）解：函数f（x）在区间（0，+∞）上单调递增，证明如下

任取x1，x2∈（0，+∞），且x1＜x2，

则f（x1）﹣f（x2）= ，

因为x1，x2∈（0，+∞），且x1＜x2，则 ，又x＞1时，f（x）＞0，

所以 ，即f（x1）＜f（x2），

函数f（x）在区间（0，+∞）上单调递增

（3）解：f（9）=f（3）+f（3）=2，

由（2）知函数f（x）在区间（0，+∞）上单调递增

不等式f（kx）+f（4﹣x）＜2可化为f（kx（4﹣x））＜f（9），因为k＞0

不等式故可化为 ，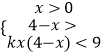

由题可得，0＜x＜4时，kx（4﹣x）＜9恒成立，

即0＜x＜4时， 恒成立， 0＜x＜4，y=x（4﹣x）∈（0，4]，

所以

所以

【解析】（1）利用赋值法即可求f（1）， 的值；（2）根据函数单调性的定义即可判断函数f（x）在区间（0，+∞）上单调性；（3）根据函数奇偶性和单调性的性质将不等式进行转化求解即可．