题目内容
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
【答案】
(1)证明:以点A为原点建立空间直角坐标系,如图,
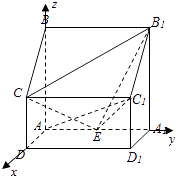
依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).
则 ![]() ,
,
而 ![]() =0.
=0.
所以B1C1⊥CE;
(2)解: ![]() ,
,
设平面B1CE的法向量为 ![]() ,
,
则 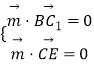 ,即
,即 ![]() ,取z=1,得x=﹣3,y=﹣2.
,取z=1,得x=﹣3,y=﹣2.
所以 ![]() .
.
由(1)知B1C1⊥CE,又CC1⊥B1C1,所以B1C1⊥平面CEC1,
故 ![]() 为平面CEC1的一个法向量,
为平面CEC1的一个法向量,
于是 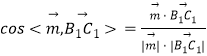 =
= ![]() .
.
从而 ![]() =
= ![]() =
= ![]() .
.
所以二面角B1﹣CE﹣C1的正弦值为 ![]() .
.
(3)解: ![]() ,
,
设 ![]() 0≤λ≤1,
0≤λ≤1,
有 ![]() .
.
取 ![]() 为平面ADD1A1的一个法向量,
为平面ADD1A1的一个法向量,
设θ为直线AM与平面ADD1A1所成的角,
则 ![]() =
= 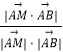
= ![]() .
.
于是 解得 所以线段AM的长为 ![]() .
.![]() .所以
.所以 ![]() .
.![]() .
.
【解析】(1)由题意可知,AD,AB,AA1两两互相垂直,以a为坐标原点建立空间直角坐标系,标出点的坐标后,求出 ![]() 和
和 ![]() ,由
,由 ![]() 得到B1C1⊥CE;(2)求出平面B1CE和平面CEC1的一个法向量,先求出两法向量所成角的余弦值,利用同角三角函数基本关系求出其正弦值,则二面角B1﹣CE﹣C1的正弦值可求;(3)利用共线向量基本定理把M的坐标用E和C1的坐标及待求系数λ表示,求出平面ADD1A1的一个法向量,利用向量求线面角的公式求出直线AM与平面ADD1A1所成角的正弦值,代入
得到B1C1⊥CE;(2)求出平面B1CE和平面CEC1的一个法向量,先求出两法向量所成角的余弦值,利用同角三角函数基本关系求出其正弦值,则二面角B1﹣CE﹣C1的正弦值可求;(3)利用共线向量基本定理把M的坐标用E和C1的坐标及待求系数λ表示,求出平面ADD1A1的一个法向量,利用向量求线面角的公式求出直线AM与平面ADD1A1所成角的正弦值,代入 ![]() 求出λ的值,则线段AM的长可求.
求出λ的值,则线段AM的长可求.

 字词句段篇系列答案
字词句段篇系列答案