题目内容
【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)y=x(2)a≤![]()
【解析】试题分析:
(1)根据导数的几何意义求解.(2)当x=0时,f(0)=0![]() 恒成立;当0<x≤
恒成立;当0<x≤![]() 时分离参数可得
时分离参数可得![]() 在
在![]() 上恒成立,设g(x)=
上恒成立,设g(x)=![]() ,x∈(0,
,x∈(0, ![]() ],利用导数可得函数g(x)的最小值为g(
],利用导数可得函数g(x)的最小值为g(![]() )=
)=![]() ,故可得a≤
,故可得a≤![]() ,即为所求范围.
,即为所求范围.
试题解析:
(1)因为f(x)=exsinx-ax2,
所以f(x)=ex(cosx+sinx)-2ax,
故f(0)=1.
又f(0)=0,
故所求切线方程为y= x.
(2)①当x=0时,f(0)=0![]() 在区间
在区间![]() 上恒成立.
上恒成立.
②当0<x≤![]() 时,由
时,由![]() 得
得![]() 在
在![]() 上恒成立.
上恒成立.
令g(x)=![]() ,x∈(0,
,x∈(0, ![]() ],
],
则g(x)=![]() .
.
令G(x)=x(sinx+cosx)-2sinx,x∈(0, ![]() ],
],
则G(x)=(cosx-sinx)(x-1),
故当0<x<![]() 时,G(x)<0,G(x)单调递减;
时,G(x)<0,G(x)单调递减;
当![]() <x<1时,G(x)>0,G(x)单调递增;
<x<1时,G(x)>0,G(x)单调递增;
当1<x≤![]() 时,G(x)<0,G(x)单调递减,
时,G(x)<0,G(x)单调递减,
又G(0)=0,G(1)=cos1-sin1<0,
所以G(x)<0,
所以g(x)<0,
所以g(x)在(0, ![]() ]上单调递减,
]上单调递减,
所以g(x)≥g(![]() )=
)=![]() ,
,
故a≤![]() .
.
综上实数![]() 的取值范围为
的取值范围为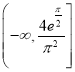 .
.

【题目】已知具有线性相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(2)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求恰有1个点落在直线![]() 右下方的概率.
右下方的概率.
参考公式: 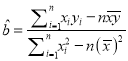 ,
, ![]() .
.
【题目】在对人们的休闲方式的一次调查中,用简单随机抽样方法调查了125人,其中女性70人,男性55人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外35人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
(3)在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座,讲座结束后再从这6人中抽取2人作反馈交流,求参加交流的恰好为2位女性的概率.
附:
P( | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
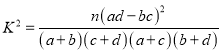
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | |||
男 | |||
合计 |