题目内容
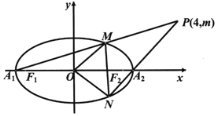
【题目】在平面直角坐标系xOy中,已知圆心在![]() 轴上的圆
轴上的圆![]() 经过两点
经过两点![]() 和
和![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)当![]() 时,
时,![]() 为直线
为直线![]() 上的定点,若圆
上的定点,若圆![]() 上存在唯一一点
上存在唯一一点![]() 满足
满足![]() ,求定点
,求定点![]() 的坐标;
的坐标;
(3)设点A,B为圆![]() 上任意两个不同的点,若以AB为直径的圆与直线
上任意两个不同的点,若以AB为直径的圆与直线![]() 都没有公共点,求实数
都没有公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意,设圆的方程为![]() ,列方程解得即可;
,列方程解得即可;
(2)根据题意,利用![]() 得点
得点![]() 的轨迹方程为
的轨迹方程为![]() ,再利用两圆相切解得即可.
,再利用两圆相切解得即可.
(3)记以![]() 为直径的圆为圆
为直径的圆为圆![]() ,设
,设![]() ,得圆
,得圆![]() 的半径
的半径![]() ,利用
,利用![]() ,表示出动点
,表示出动点![]() 的轨迹为以
的轨迹为以![]() 为圆心,
为圆心,![]() 为半径的圆的内部(含边界),再利用点C到直线l的距离
为半径的圆的内部(含边界),再利用点C到直线l的距离![]() ,解得即可.
,解得即可.
(1)设圆的方程为![]() ,将M,N坐标带入,
,将M,N坐标带入,
得: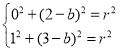 ,解得
,解得![]() ,
,
所以圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,由
,由![]() ,即
,即![]() ,
,
化简得![]() ,
,
由题意,此圆与圆C相切,故![]() ,解得
,解得![]() ,
,
所以![]() 或
或![]()
(3)记以AB为直径的圆为圆M,设圆M上有一动点![]() ,
,
设![]() ,则圆M的半径
,则圆M的半径![]() ,于是
,于是![]()
,其中![]() 为
为![]() 的夹角,
的夹角,![]() .
.
因为![]() ,所以
,所以![]() .
.
故点![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆的内部(含边界),
为半径的圆的内部(含边界),
所以点C到直线l的距离![]() ,即
,即![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目