题目内容
【题目】在对人们的休闲方式的一次调查中,用简单随机抽样方法调查了125人,其中女性70人,男性55人.女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外35人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
(3)在休闲方式为看电视的人中按分层抽样方法抽取6人参加某机构组织的健康讲座,讲座结束后再从这6人中抽取2人作反馈交流,求参加交流的恰好为2位女性的概率.
附:
P( | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
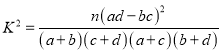
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | |||
男 | |||
合计 |
【答案】(1)答案见解析;(2)在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”.(3)0.4.
【解析】【试题分析】(1)根据题目所给已知条件填写好![]() 联表;(2)通过计算
联表;(2)通过计算![]() ,所以在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”. (3)按分层抽样,则男性有
,所以在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”. (3)按分层抽样,则男性有![]() 人,女性有
人,女性有![]() 人,通过列举法可求得基本事件总数有
人,通过列举法可求得基本事件总数有![]() 种,符合要求的有
种,符合要求的有![]() 种,故概率为
种,故概率为![]() .
.
【试题解析】
(1) ![]() 列联表为:
列联表为:
休闲方式 性别 | 看电视 | 运动 | 合计 |
女 | 40 | 30 | 70 |
男 | 20 | 35 | 55 |
合计 | 60 | 65 | 125 |
(2)假设“休闲方式与性别无关”,计算
![]() .
.
因为![]() ,所以在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”.
,所以在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”.
(3)休闲方式为看电视的共60人,按分层抽样方法抽取6人,则男性有2人,可记为A、B,女性4人,可记为c,d,e、f.
现从6人中抽取2人,基本事件是AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种不同的方法,恰是2女性的有cd、ce、cf、de、df、ef共6种不同的方法,故所求概率为![]() .
.


