Question

【题目】如图，三棱柱ABC－A1B1C1中，底面ABC为等腰直角三角形，AB＝AC＝1，BB1＝2，∠ABB1＝60°.

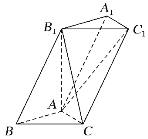
(I) 证明：AB⊥平面AB1C；

(II) 若B1C＝2，求AC1与平面BCB1所成角的正弦值.

Answer 1

【答案】(I)详见解析(II)

【解析】

（Ⅰ）连结AB1，在△ABB1中，由余弦定理得求出AB1，通过计算勾股定理证明AB1⊥AB，以及证明AC⊥AB，推出AB⊥平面AB1C．得到AB⊥B1C．

（Ⅱ）以A为原点，以的方向分别为x轴，y轴，z轴的正方向建立空间直角坐标系，求出平面BCB1的法向量，利用向量的数量积求解AC1与平面BCB1所成角的正弦值．

(I)证明:连接AB1，在△ABB1中，AB＝1，BB1＝2，∠ABB1＝60°，

由余弦定理得，AB＝AB2＋BB－2AB·BB1·cos∠ABB1＝3，

∴AB1＝，∴BB＝AB2＋AB，

∴AB1⊥AB.

又△ABC为等腰直角三角形，且AB＝AC，

∴AC⊥AB，∵AC∩AB1＝A，

∴AB⊥平面AB1C.

(II)解:∵AB1＝，AB＝AC＝1，B1C＝2，

∴B1C2＝AB＋AC2，∴AB1⊥AC.

如图，以A为原点，以，，的方向分别为x轴，y轴，z轴的正方向建立空间直角坐标系，则A(0，0，0)，B1(0，0，)，

B(1，0，0)，C(0，1，0)，

∴＝(－1，0，)，

＝(－1，1，0).

设平面BCB1的一个法向量为n＝(x，y，z)，

由得令z＝1，得x＝y＝，

∴平面BCB1的一个法向量为n＝(，，1).

∵＝＋＝＋＝(0，1，0)＋(－1，0，)＝(－1，1，)，

∴cos〈，n〉＝＝＝，

∴AC1与平面BCB1所成角的正弦值为.