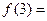题目内容
已知x1,x2是关于x的一元二次方程x2-(m-1)x-(m-1)=0的两个解,设y=f(m)=(x1+x2)2-x1x2,求函数y=f(m)的解析式及值域.
由题意知,x1,x2是关于x的一元二次方程x2-(m-1)x-(m-1)=0的两个解,
∴x1+x2=m-1,x1•x2=-m+1,且△=(m-1)2+4(m-1)≥0,解得m≤-3或m≥1,
∵y=f(m)=(x1+x2)2-x1x2,
∴y=f(m)=(m-1)2+m-1=m2-m=(m-
)2-
,
∵m≤-3或m≥1,∴当m=1时,函数取到最小值是0,
∴此函数的值域是[0,+∞).
∴x1+x2=m-1,x1•x2=-m+1,且△=(m-1)2+4(m-1)≥0,解得m≤-3或m≥1,
∵y=f(m)=(x1+x2)2-x1x2,
∴y=f(m)=(m-1)2+m-1=m2-m=(m-
| 1 |
| 2 |
| 1 |
| 4 |
∵m≤-3或m≥1,∴当m=1时,函数取到最小值是0,
∴此函数的值域是[0,+∞).

练习册系列答案
相关题目
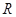 上的奇函数
上的奇函数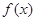 ,当
,当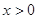 时,
时,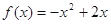
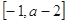 上单调递增,求实数
上单调递增,求实数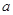 的取值范围。
的取值范围。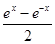 ,x∈R
,x∈R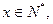
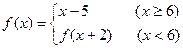 ,则
,则