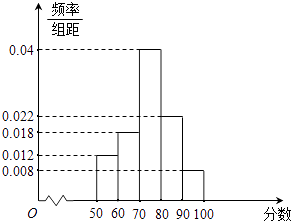
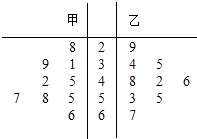
题目内容
【题目】已知圆心C（1，2），且经过点（0，1） （Ⅰ）写出圆C的标准方程；
（Ⅱ）过点P（2，﹣1）作圆C的切线，求切线的方程及切线的长．
【答案】解（Ⅰ）∵圆心C（1，2），且经过点（0，1） 圆C的半径 
，
∴圆C的标准方程：（x﹣1）2+（y﹣2）2=2，
（Ⅱ）设过点P（2，﹣1）的切线方程为y+1=k（x﹣2），
即kx﹣y﹣2k﹣1=0，有： 
，
∴k2﹣6k﹣7=0，解得k=7或k=﹣1，
∴所求切线的方程为7x﹣y﹣15=0或x+y﹣1=0，
由圆的性质可知： 
【解析】（Ⅰ）求出圆的半径，即可写出圆C的标准方程；（Ⅱ）利用点斜式设出过点P（2，﹣1）作圆C的切线方程，通过圆心到切线的距离等于半径，求出切线的斜率，然后求出方程，通过切线的长、半径以及圆心与P点的距离满足勾股定理，求出切线长．
【考点精析】关于本题考查的圆的标准方程，需要了解圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程才能得出正确答案．
练习册系列答案
相关题目
