题目内容
【题目】从装有大小相同的2个红球和6个白球的袋子中，每摸出2个球为一次试验，直到摸出的球中有红球（不放回），则试验结束.
（1）求第一次试验恰摸到一个红球和一个白球概率；
（2）记试验次数为
，求的分布列及数学期望
．
【答案】（1）
；（2）
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
【解析】
试题分析：（1）由题意知，袋子中共有8个球，记“第一次试验恰摸到一个红球和一个白球”为事件A，则根据古典概型计算公式，得
.
（2）由题意知，每次试验中不放回地摸出两个球，直到摸出的球中有红球，因为袋中只有两个红球，所以最多需要进行四次试验，第一次试验的结果可能有“一个红球一个白球”或“两个红球”，第二次试验要在第一次试验没有出红球情况下进行，则袋中剩下4个白球和2个红球，结果可能为“一个红球一个白球”或“两个红球”，同理第三次试验要在前两次没有出现红球下进行，则袋中剩下2个白球和2个红球，结果能为“一个红球一个白球”或“两个红球”，第四次试验要在前三次试验没有出现红球下进行，则袋中只剩下2个红球，结果为“两个红球”，所以
的值为1、2、3、4，根据古典概型的计算公式，得
，
，
，
，从而可列出的分布列，并求出其数学期望
.
试题解析：（1）
（2）由题意可知的值分别为1、2、3、4，则，，，
所以的分布列为
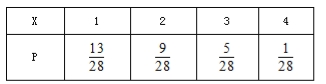
的数学期望.
练习册系列答案
相关题目
