题目内容
已知四棱锥P-ABCD,底面ABCD是 ,边长为
,边长为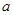 的菱形,又
的菱形,又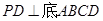 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
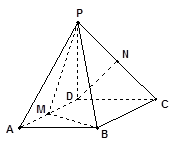
(1)证明:DN//平面PMB;
(2)证明:平面PMB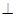 平面PAD.
平面PAD.
 ,边长为
,边长为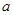 的菱形,又
的菱形,又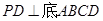 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.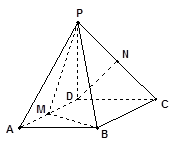
(1)证明:DN//平面PMB;
(2)证明:平面PMB
 平面PAD.
平面PAD.(1)证明见解析;(2)证明见解析.
试题分析:(1)首先取
 中点
中点 ,然后利用三角形中位线定理与平行四边形证明
,然后利用三角形中位线定理与平行四边形证明 ,最后利用直线与平面平行的判定定理.(2)转化为证明
,最后利用直线与平面平行的判定定理.(2)转化为证明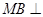 平面
平面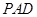 ,进而转化为证明
,进而转化为证明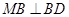 (由正三角形三线合一可证)和
(由正三角形三线合一可证)和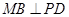 ,而证明
,而证明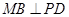 可转化为证明
可转化为证明 平面
平面 (已知).
(已知).试题解析:(1)证明:取
 中点
中点 ,连结
,连结 ,
,
因为
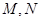 分别是棱
分别是棱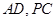 中点,所以
中点,所以 ,且
,且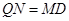 ,于是
,于是 .
.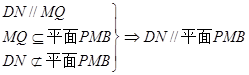 .
.(2)

又因为底面
 是
是 、边长为
、边长为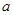 的菱形,且
的菱形,且 为
为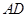 中点,
中点,所以
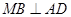 .
.又
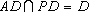 ,所以
,所以 .
.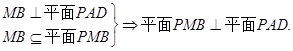

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
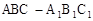 中,
中,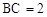 ,
,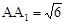 ,D、E分别是
,D、E分别是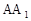 、
、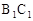 的中点,
的中点,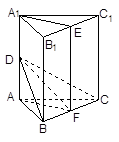
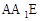 ⊥面BCD;
⊥面BCD;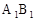 与平面BCD所成的角.
与平面BCD所成的角.
 外一点可以作无数条直线与平面
外一点可以作无数条直线与平面 垂直平面
垂直平面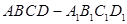 中,线段
中,线段 上(不包括端点)各有一点
上(不包括端点)各有一点 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( ) 四点共面
四点共面 与平面
与平面 所成的角为定值
所成的角为定值
 的大小为
的大小为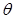 ,则
,则 的最小值为
的最小值为
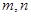 是不重合的直线,
是不重合的直线, 是不重合的平面,有下列命题:
是不重合的平面,有下列命题: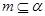 ,
,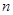 ∥
∥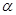 ,则
,则 ∥
∥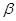 ,则
,则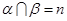 ,
,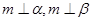 ,则
,则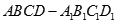 中,
中,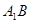 与平面
与平面 所成的角的大小是
所成的角的大小是