题目内容
已知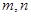 是不重合的直线,
是不重合的直线, 是不重合的平面,有下列命题:
是不重合的平面,有下列命题:
①若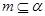 ,
,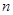 ∥
∥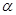 ,则
,则 ∥
∥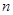 ;
;
②若 ∥
∥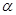 ,
, ∥
∥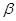 ,则
,则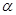 ∥
∥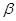 ;
;
③若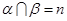 ,
, ∥
∥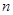 ,则
,则 ∥
∥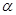 且
且 ∥
∥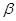 ;
;
④若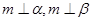 ,则
,则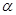 ∥
∥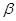
其中真命题的个数是( )
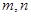 是不重合的直线,
是不重合的直线, 是不重合的平面,有下列命题:
是不重合的平面,有下列命题:①若
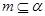 ,
,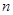 ∥
∥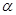 ,则
,则 ∥
∥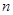 ;
;②若
 ∥
∥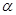 ,
, ∥
∥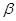 ,则
,则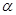 ∥
∥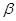 ;
;③若
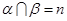 ,
, ∥
∥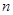 ,则
,则 ∥
∥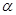 且
且 ∥
∥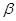 ;
;④若
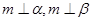 ,则
,则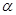 ∥
∥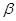
其中真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
B
试题分析:①若
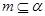 ,
,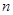
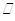
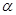 ,则
,则 与
与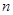 平行或异面,故不正确;②若
平行或异面,故不正确;②若
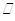
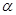 ,
,
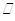
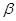 ,则
,则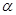 与
与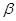 可能相交或平行,故不正确;③若
可能相交或平行,故不正确;③若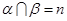 ,
,
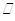
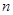 ,则
,则
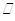
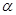 且
且
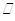
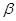 ,
, 也可能在平面内,故不正确;④若
也可能在平面内,故不正确;④若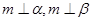 ,则
,则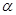
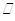
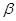 ,垂直与同一直线的两平面平行,故正确,故选B.
,垂直与同一直线的两平面平行,故正确,故选B.
练习册系列答案
相关题目
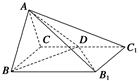
 为正方形,四边形
为正方形,四边形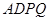 是直角梯形,
是直角梯形, ,
,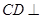 平面
平面 .
.
 平面
平面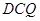 ;
;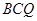 与平面
与平面 ,边长为
,边长为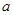 的菱形,又
的菱形,又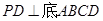 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.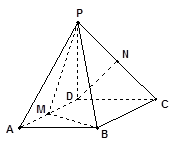
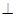 平面PAD.
平面PAD.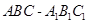 中,
中, ,
,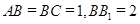 ,求:
,求: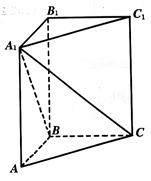
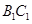 与
与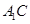 所成角的余弦值;
所成角的余弦值; 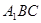 的距离.
的距离.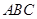 中,
中,  =900 ,
=900 , ="6,"
="6," 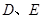 分别是
分别是 ,
,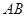 上的点,
上的点,
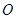 为
为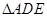 沿
沿 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎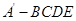 ,其中
,其中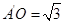


 ;
;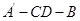 的平面角的余弦值.
的平面角的余弦值. ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.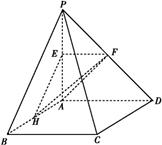
 BC,点D是BC边的中点,点E是线段AD上一点,且AE=3DE,点M是线段SD上一点,
BC,点D是BC边的中点,点E是线段AD上一点,且AE=3DE,点M是线段SD上一点,
 、
、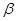 ,直线
,直线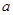 、
、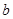 ,
,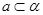 ,
,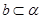 ,则“
,则“ ,
,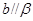 ”是“
”是“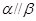 ”的( )
”的( )