题目内容
在四棱锥P-ABCD中,AB∥DC,AB⊥平面PAD, PD=AD,AB=2DC,E是PB的中点.

求证:(1)CE∥平面PAD;
(2)平面PBC⊥平面PAB.

求证:(1)CE∥平面PAD;
(2)平面PBC⊥平面PAB.
(1)详见解析; (2)详见解析.
试题分析:(1)要证明线面平行根据线面平行的判定定理可将问题转化为证明平面外直线平行与平面内一条直线,则此问题关键即为找出这条直线,又由题中所给:AB=2DC,E是PB的中点,不难想到取PA的中点,进而运用三角形的中位线构造平行关系,问题即可得证; (2)中要证明面面垂直由面面垂直的判定定理可知将问题转化为证明线面垂直,结全题中所给条件和(1)中已证明的过程,不难发现可转化为去证:
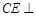 平面PAB,再根据线面垂直的判定定理可转化为证线线垂直:
平面PAB,再根据线面垂直的判定定理可转化为证线线垂直: ,
, ,这样问题即可得证.
,这样问题即可得证.试题解析:(1)取PA的中点F,连EF,DF. 2分
因为E是PB的中点,所以EF // AB,且
 .
.因为AB∥CD,AB=2DC,所以EF∥CD, 4分
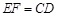 ,于是四边形DCEF是平行四边形,
,于是四边形DCEF是平行四边形,从而CE∥DF,而
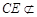 平面PAD,
平面PAD,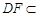 平面PAD,
平面PAD,故CE∥平面PAD. 7分
(2)因为PD=AD,且F是PA的中点,所以
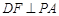 .
.因为AB⊥平面PAD,
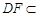 平面PAD,所以
平面PAD,所以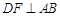 . 10分
. 10分因为CE∥DF,所以
 ,
, .
.因为
 平面PAB,
平面PAB, ,所以
,所以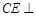 平面PAB.
平面PAB.因为
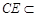 平面PBC,所以平面PBC⊥平面PAB. 14分
平面PBC,所以平面PBC⊥平面PAB. 14分
练习册系列答案
相关题目
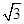 ,D是AC的中点.
,D是AC的中点.
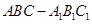 是直棱柱,
是直棱柱,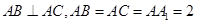 .点
.点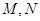 分别为
分别为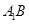 和
和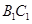 的中点.
的中点. 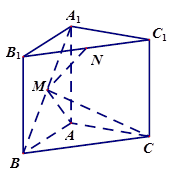
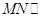 平面
平面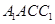 ;
;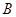 到平面
到平面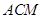 的距离.
的距离.  为正方形,四边形
为正方形,四边形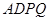 是直角梯形,
是直角梯形, ,
,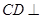 平面
平面 .
.
 平面
平面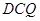 ;
;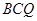 与平面
与平面 在平面
在平面 内,
内, ,
,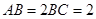 ,P为平面
,P为平面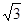 ,
,
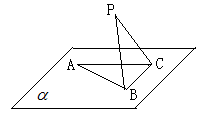
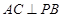
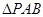 的面积取得最大值时,求直线BC与平面PAB所成角的大小
的面积取得最大值时,求直线BC与平面PAB所成角的大小 ,边长为
,边长为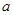 的菱形,又
的菱形,又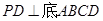 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.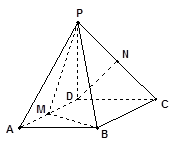
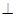 平面PAD.
平面PAD.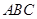 中,
中,  =900 ,
=900 , ="6,"
="6," 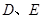 分别是
分别是 ,
,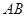 上的点,
上的点,
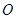 为
为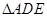 沿
沿 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎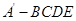 ,其中
,其中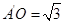


 ;
;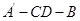 的平面角的余弦值.
的平面角的余弦值.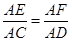 =λ(0<λ<1).
=λ(0<λ<1).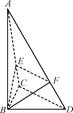
 、
、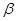 ,直线
,直线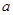 、
、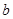 ,
,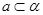 ,
,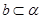 ,则“
,则“ ,
,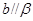 ”是“
”是“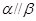 ”的( )
”的( )