题目内容
已知椭圆 经过点
经过点 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点 在
在 轴上,离心率
轴上,离心率 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求 的角平分线所在直线
的角平分线所在直线 的方程;
的方程;
(Ⅲ)在椭圆 上是否存在关于直线
上是否存在关于直线 对称的相异两点?
对称的相异两点?
若存在,请找出;若不存在,说明理由.
 经过点
经过点 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点 在
在 轴上,离心率
轴上,离心率 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)求
 的角平分线所在直线
的角平分线所在直线 的方程;
的方程;(Ⅲ)在椭圆
 上是否存在关于直线
上是否存在关于直线 对称的相异两点?
对称的相异两点?若存在,请找出;若不存在,说明理由.

(1)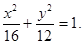 (2)
(2)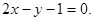 (3)不存在满足题设条件的点B和C.
(3)不存在满足题设条件的点B和C.
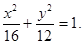 (2)
(2)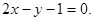 (3)不存在满足题设条件的点B和C.
(3)不存在满足题设条件的点B和C.有关解析几何的问题,常常涉及曲线的方程,此时往往要注意利用有关曲线的定义来解决,同时还会涉及直线与有关曲线的交点问题,在处理过程中往往需要结合二次方程的根与系数的关系解决
(I)设椭圆E的方程为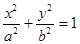 ,
,
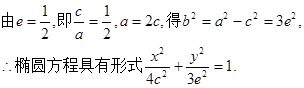
将A(2,3)代入上式,得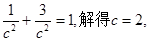
∴椭圆E的方程为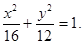
(II)解法1:由(I)知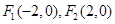 ,所以直线AF1的方程为:
,所以直线AF1的方程为: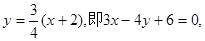 直线AF2的方程为:
直线AF2的方程为: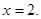 由点A在椭圆E上的位置知,直线l的斜率为正数.设
由点A在椭圆E上的位置知,直线l的斜率为正数.设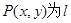 上任一点,则
上任一点,则
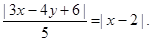 若
若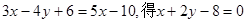 (因其斜率为负,舍去).
(因其斜率为负,舍去).
所以直线l的方程为: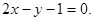
解法2:
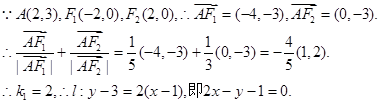
(III)解法1:
假设存在这样的两个不同的点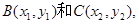
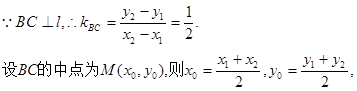
由于M在l上,故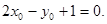 ①
①
又B,C在椭圆上,所以有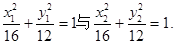 两式相减,得
两式相减,得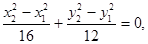
即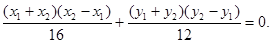 将该式写为
将该式写为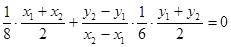 ,并将直线BC的斜率
,并将直线BC的斜率 和线段BC的中点,表示代入该表达式中,得
和线段BC的中点,表示代入该表达式中,得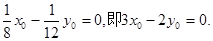 ②
②
①×2—②得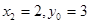 ,即BC的中点为点A,而这是不可能的.
,即BC的中点为点A,而这是不可能的.
∴不存在满足题设条件的点B和C.
解法2:假设存在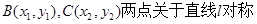 ,则
,则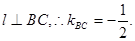
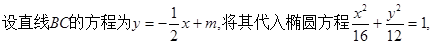 得一元二次方程
得一元二次方程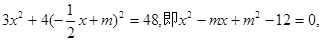 则
则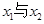 是该方程的两个根,由韦达定理得
是该方程的两个根,由韦达定理得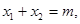 于是
于是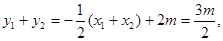 ∴B,C的中点坐标为
∴B,C的中点坐标为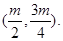 又线段BC的中点在直线
又线段BC的中点在直线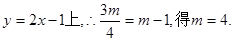
即B,C的中点坐标为(2,3),与点A重合,矛盾.∴不存在满足题设条件的相异两点.
(I)设椭圆E的方程为
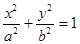 ,
,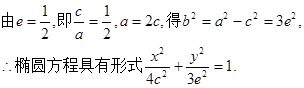
将A(2,3)代入上式,得
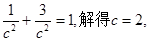
∴椭圆E的方程为
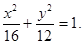
(II)解法1:由(I)知
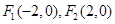 ,所以直线AF1的方程为:
,所以直线AF1的方程为: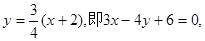 直线AF2的方程为:
直线AF2的方程为: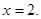 由点A在椭圆E上的位置知,直线l的斜率为正数.设
由点A在椭圆E上的位置知,直线l的斜率为正数.设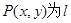 上任一点,则
上任一点,则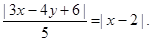 若
若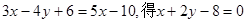 (因其斜率为负,舍去).
(因其斜率为负,舍去).所以直线l的方程为:
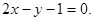
解法2:
(III)解法1:
假设存在这样的两个不同的点
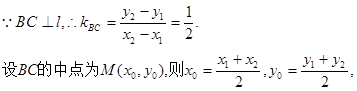
由于M在l上,故
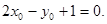 ①
①又B,C在椭圆上,所以有
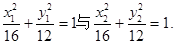 两式相减,得
两式相减,得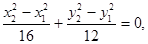
即
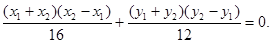 将该式写为
将该式写为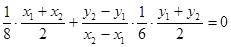 ,并将直线BC的斜率
,并将直线BC的斜率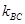 和线段BC的中点,表示代入该表达式中,得
和线段BC的中点,表示代入该表达式中,得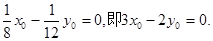 ②
②①×2—②得
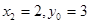 ,即BC的中点为点A,而这是不可能的.
,即BC的中点为点A,而这是不可能的.∴不存在满足题设条件的点B和C.
解法2:假设存在
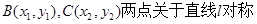 ,则
,则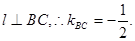
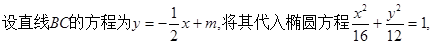 得一元二次方程
得一元二次方程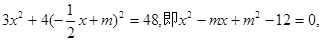 则
则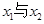 是该方程的两个根,由韦达定理得
是该方程的两个根,由韦达定理得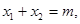 于是
于是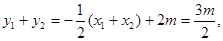 ∴B,C的中点坐标为
∴B,C的中点坐标为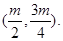 又线段BC的中点在直线
又线段BC的中点在直线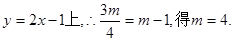
即B,C的中点坐标为(2,3),与点A重合,矛盾.∴不存在满足题设条件的相异两点.

练习册系列答案
相关题目
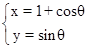 (θ为参数)的圆心到直线l:
(θ为参数)的圆心到直线l: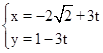 (t为参数)的距离为 .
(t为参数)的距离为 . 是半圆的直径,弦
是半圆的直径,弦 和弦
和弦 相交于点
相交于点 ,且
,且 ,则
,则 .
.

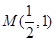 的直线
的直线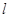 与圆C:
与圆C: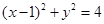 交于
交于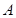 、
、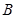 两点,
两点,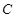 为圆心,当
为圆心,当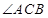 最小时,直线
最小时,直线 的半径为
的半径为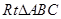 的两条直角边
的两条直角边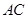 ,
,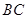 的长分别为
的长分别为 ,
,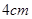 ,以
,以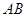 交于点
交于点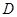 ,则
,则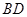 =
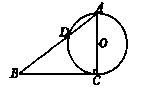
= 
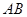 是圆
是圆 的直径,
的直径, ,
, ,则
,则 ;
;