题目内容
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数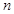 及天数如下表:
及天数如下表:
售出个数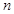 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(1)计算小王某天售出该现烤面包超过13个的概率;
(2)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(3)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
(1)0.5;(2)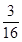 ;(3)分布列为
;(3)分布列为利润 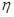
80 95 110 125 140 概率 
0.1 0.1 0.1 0.2 0.5
数学期望为123.5元.
解析试题分析:(1)由于小王某天售出该现烤面包超过13个的情况有三种:恰14个和恰15个,由题中表格易得:小王某天售出该现烤面包恰14个和恰15个的概率分别为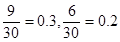 ,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.
,再由小王某天售出该现烤面包恰14个和恰15个这两个事件是互斥的,所以小王某天售出该现烤面包超过13个的概率就等于上述两个概率之和为:0.3+0.2=0.5.
(2)设在最近的5天中售出超过13个的天数为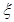 ,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以
,由于每天售出的个数要么超过13个,要么不超过13个只有这两种结果,且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变各为0.5,所以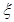 服从参数为5和0.5的二项分布,即
服从参数为5和0.5的二项分布,即 ,从而事件“小王增加订购量”的概率,即是
,从而事件“小王增加订购量”的概率,即是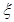 >3的概率,而
>3的概率,而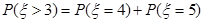 ,再由二项分布的概率公式
,再由二项分布的概率公式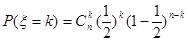 可算得事件“小王增加订购量”的概率;
可算得事件“小王增加订购量”的概率;
(3)由于小王每天订购14个现烤面包,则可设其一天的利润为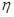 元,由已知求出
元,由已知求出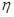 的所有可能取值,并结合题只所给条件可得到
的所有可能取值,并结合题只所给条件可得到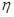 的每一个可能取值的概率,从而求得其分布列,在由数学期望公式:
的每一个可能取值的概率,从而求得其分布列,在由数学期望公式: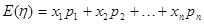 就可求得所获利润的数学期望.
就可求得所获利润的数学期望.
试题解析:(1)记事件A=“小王某天售出超过13个现烤面包”, 1分
用频率估计概率可知: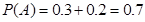 . 2分
. 2分
所以小王某天售出超过13个现烤面包的概率为0.5. 3分
(2)设在最近的5天中售出超过13个的天数为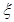 ,
,
则 . ..5分
. ..5分
记事件B=“小王增加订购量”,
则有 ,
,
所以小王增加订购量的概率为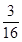 . 8分
. 8分
(3)若小王每天订购14个现烤面包,设其一天的利润为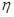 元,则
元,则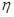 的所有可能取值为80,95,110,125,140. 9分
的所有可能取值为80,95,110,125,140. 9分
其分布列为
11分 利润 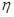
80 95 110 125 140 概率 
0.1 0.1 0.1 0.2 0.5
则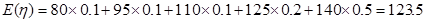
所以小王每天出售该现烤面包所获利润的数学期望为123.5元. ..13分
考点:1.概率和公式;2.二项分布;3.分布列与数学期望.

为了解七班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
 .(12分)
.(12分)(1)请将上面的列联表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为
 ,求
,求 的分布列与期望.
的分布列与期望.下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05[ | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:
 ,其中
,其中 )
)

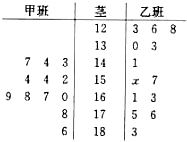
 、
、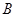 两盒中都有红球、白球,且球的形状、大小都相同,盒子
两盒中都有红球、白球,且球的形状、大小都相同,盒子 个红球与
个红球与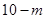 个白球,盒子
个白球,盒子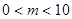 ).
). 表示红球的个数;
表示红球的个数;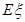 等于定值;
等于定值;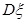 取到最小值,并求出最小值.
取到最小值,并求出最小值.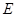 :在第一次取到红球后,以后两次都取到白球,事件
:在第一次取到红球后,以后两次都取到白球,事件 :在第一次取到白球后,以后两次都取到红球,若概率
:在第一次取到白球后,以后两次都取到红球,若概率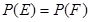 ,求
,求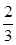 ,乙获胜的概率为
,乙获胜的概率为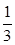 ,各局比赛结果相互独立.
,各局比赛结果相互独立.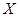 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求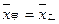 ,方差
,方差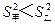 ,则成绩较稳定的同学是 (填“甲”或“乙”)
,则成绩较稳定的同学是 (填“甲”或“乙”)