题目内容
甲有大小相同的两张卡片,标有数字2、3;乙有大小相同的卡片四张,分别标有1、2、3、4.
(1)求乙随机抽取的两张卡片的数字之和为奇数的概率;
(2)甲、乙分别取出一张卡,比较数字,数字大者获胜,求乙获胜的概率.
(1) ;(2)
;(2)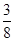 .
.
解析试题分析:(1)两张卡片的数字之和为奇数,即一奇一偶;两张卡片的数字之和为偶数,即两奇或两偶;(2)乙获胜,即要求乙取出的卡片上标有的数字比甲取出的卡片上标有的数字大,这样的情形有多少种,往往需要用枚举法.在(1)中我们是不考虑两张卡片的顺序的,若考虑顺序,即原题(1)这样表述:求乙随机先后抽取的两张卡片的数字之和为奇数的概率,则应这样求解:基本事件总数为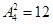 ,同时两张卡片的数字之和为奇数,即分为先奇后偶和先偶后奇,共
,同时两张卡片的数字之和为奇数,即分为先奇后偶和先偶后奇,共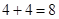 种,概率为
种,概率为 ,所以概率计算一定要分清与顺序是否有关.
,所以概率计算一定要分清与顺序是否有关.
试题解析:(1)乙随机在分别标有1、2、3、4的四张卡片中抽取的两张卡片,其基本事件共有 种,若要求两张卡片的数字之和为奇数,即一张为奇数,即在1、3中抽一张,另一张为偶数,即在2、4中抽一张,则两张卡片的数字之和为奇数这样的事件含有
种,若要求两张卡片的数字之和为奇数,即一张为奇数,即在1、3中抽一张,另一张为偶数,即在2、4中抽一张,则两张卡片的数字之和为奇数这样的事件含有 基本事件,根据古典概型概率计算公式的概率为
基本事件,根据古典概型概率计算公式的概率为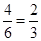 . 5分
. 5分
(2)甲、乙分别取出一张卡,则基本事件总数为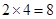 ,乙获胜,即要求乙取出的卡片上标有的数字比甲取出的卡片上标有的数字大,故符合条件的数对有
,乙获胜,即要求乙取出的卡片上标有的数字比甲取出的卡片上标有的数字大,故符合条件的数对有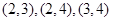 ,有3对,根据古典概型概率计算公式得乙获胜的概率为
,有3对,根据古典概型概率计算公式得乙获胜的概率为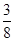 . 10分
. 10分
考点:计数原理与古典概型.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案某校夏令营有3名男同学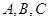 和3名女同学
和3名女同学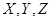 ,其年级情况如下表:
,其年级情况如下表:
| | 一年级 | 二年级 | 三年级 |
| 男同学 |  | 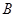 | 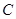 |
| 女同学 | 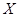 | 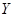 | 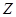 |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母列举出所有可能的结果
(2)设
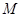 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件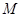 发生的概率.
发生的概率. 为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为2/3
⑴请将上面列连表补充完整,并判断是否有
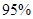 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望.
附:
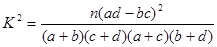 ,其中
,其中 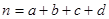
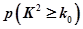 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数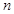 及天数如下表:
及天数如下表:
售出个数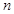 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(1)计算小王某天售出该现烤面包超过13个的概率;
(2)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量.试求小王增加订购量的概率.
(3)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
 .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求:
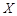 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
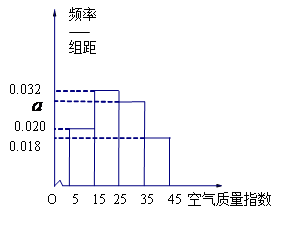
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为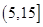 ,
,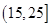 ,
,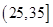 ,
,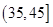 ,由此得到样本的空气质量指数频率分布直方图,如图.
,由此得到样本的空气质量指数频率分布直方图,如图.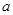 的值;
的值; 组的频率为
组的频率为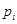 ,第
,第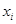
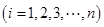 ,则样本数据的平均值为
,则样本数据的平均值为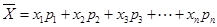 .)
.) ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取
,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取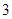 天的数值,其中达到“特优等级”的天数为
天的数值,其中达到“特优等级”的天数为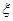 ,求
,求